(本小题满分16分)
已知数列 满足
满足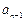 +
+ =4n-3(n∈
=4n-3(n∈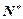 ).
).
(1)若数列 是等差数列,求
是等差数列,求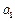 的值;
的值;
(2)当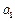 =2时,求数列
=2时,求数列 的前n项和
的前n项和 ;
;
(3)若对任意n∈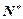 ,都有
,都有 ≥5成立,求
≥5成立,求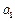 的取值范围.
的取值范围.
直线 与椭圆
与椭圆 交于A、B两点,记△ABO的面积为S.
交于A、B两点,记△ABO的面积为S.
(1)求在k = 0,0 < b < 1的条件下,S的最大值;
(2)当 | AB | = 2,S = 1时,求直线AB的方程.
某集团设资兴办甲、乙两个企业,2005年甲企业获利润32万元,乙企业获利润72万元,以后每年甲企业的利润以上一年的1.5倍递增.而乙企业的利润是上一年利润的 ,预期目标为两企业年利润之和为160万元,以2006年初起.
,预期目标为两企业年利润之和为160万元,以2006年初起.
(1)哪一年两企业获利之和最小,最小值为多少?
(2)经过几年可以达到预期目标?(精确到年)
已知 在曲线
在曲线 上(
上( ),且
),且
(1)求数列 的通项公式;
的通项公式;
(2)设数列 的前n项和为Tn,且满足
的前n项和为Tn,且满足 ,试确定b1的值,使得
,试确定b1的值,使得 是等差数列.
是等差数列.
已知 为实常数),且
为实常数),且 ,其图象和y轴交于A点;数列
,其图象和y轴交于A点;数列 为公差为
为公差为 的等差数列,且
的等差数列,且 ;点列
;点列
(1)求函数 的表达式;
的表达式;
(2)设 为直线
为直线 的斜率,
的斜率, 的斜率,求证数
的斜率,求证数 仍为等差数列;
仍为等差数列;
(3)已知m为一给定自然数,常数a满足 ,求证数列
,求证数列 有唯一的最大项.
有唯一的最大项.
已知椭圆 ,通径长为1,且焦点与短轴两端点构成等边三角形,(1)求椭圆的方程;(2)过点Q(-1,0)的直线l交椭圆于A,B两点,交直线x=-4于点E,点Q分
,通径长为1,且焦点与短轴两端点构成等边三角形,(1)求椭圆的方程;(2)过点Q(-1,0)的直线l交椭圆于A,B两点,交直线x=-4于点E,点Q分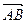 所成比为λ,点E分
所成比为λ,点E分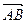 所成比为μ,求证λ+μ为定值,并计算出该定值.
所成比为μ,求证λ+μ为定值,并计算出该定值.