(本大题共14分)
已知函数 (
( 为实常数)的两个极
为实常数)的两个极 值点为
值点为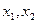 ,且满足
,且满足
(1)求 的取值范围;
的取值范围;
(2)比较 与
与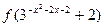 的大小.
的大小.
(本小题满分12分)
已知A  ,
,

(1)求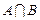 和
和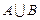 ;
;
(2)若记符号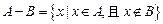 ,
,
①在图中把表示“集合 ”的部分用阴影涂黑;
”的部分用阴影涂黑;
②求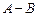 和
和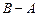 .
.
(本 小题满分14分)
小题满分14分)
已知定义在 的函数
的函数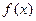 同时满足以下三条:①对任意的
同时满足以下三条:①对任意的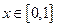 ,总有
,总有 ;②
;② ;③当
;③当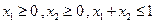 时,总有
时,总有 成立.
成立.
(1)函数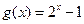 在区间
在区间 上是否同时适合①②③?并说明理由;
上是否同时适合①②③?并说明理由;
(2)设 ,且
,且 ,试比较
,试比较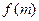 与
与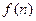 的大小;
的大小;
(3)假设存在 ,使得
,使得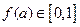 且
且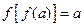 ,求证:
,求证: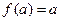 .
.
(本小题满分13分)
甲、乙两公司同时开发同一种新产品,经测算,对于函数 ,
,
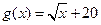 ,当甲公司投入
,当甲公司投入 万元作宣传时,若乙公司投入的宣传费小于
万元作宣传时,若乙公司投入的宣传费小于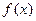 万元,则乙公司对这一新产品的开发有失败的风险,否则没有失败的风险;当乙公
万元,则乙公司对这一新产品的开发有失败的风险,否则没有失败的风险;当乙公
 司投入
司投入 万元作宣传时,若甲公司投入的宣传费小于
万元作宣传时,若甲公司投入的宣传费小于 万元,则甲公司对这一新产品的开发有失败的风险,否则没有失败的风险.
万元,则甲公司对这一新产品的开发有失败的风险,否则没有失败的风险.
(1)当甲公司不投入宣传费时,乙公司要避免新产品的开发有失败风险,至少要投入多少万元宣传费?
(2)若甲、乙公司为了避免恶性竞争,经过协商,同意在双方均无失败风险的情况下尽可能少地投入宣传 费用,问甲、乙两公司应投入多少宣传费?
费用,问甲、乙两公司应投入多少宣传费?
(本小题满分12分)
(1)设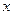 是正实数,求证:
是正实数,求证: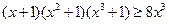 ;
;
(2)若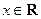 ,不等式
,不等式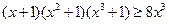 是否仍然成立?如果成立,请给出证明;如果不成立,请举出一个使它不成立的
是否仍然成立?如果成立,请给出证明;如果不成立,请举出一个使它不成立的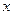 的值.
的值.
(本小题满分12分) 数列
数列 的前
的前 项和为
项和为 且
且 .
.
(1)求数列 的通项公式;
的通项公式;
(2)等差数列 的各项均为正数,其前
的各项均为正数,其前 项和为
项和为 ,
, ,又
,又 成等比数列,求
成等比数列,求 .
.