(本题满分12分)
已知椭圆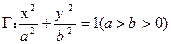 的左、右焦点为
的左、右焦点为 ,过点
,过点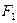 斜率为正数的直线交
斜率为正数的直线交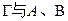 两点,且
两点,且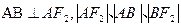 成等差数列。
成等差数列。
(Ⅰ)求 的离心率;
的离心率;
(Ⅱ)若直线y=kx(k<0)与 交于C、D两点,求使四边形ABCD面积S最大时k的值。
交于C、D两点,求使四边形ABCD面积S最大时k的值。
在数列中,a1=2,an+1=4an-3n+1,n∈N*.
(1)证明数列是等比数列;
(2)求数列的前n项和Sn;
(3)证明不等式Sn+1≤4Sn,对任意n∈N*皆成立
用反证法证明:如果a>b>0,那么>.
将正△ABC分割成n2(n≥2,n∈N)个全等的小正三角形(图乙,图丙分别给出了n=2,3的情形),在每个三角形的顶点各放置一个数,使位于△ABC的三边及平行于某边的任一直线上的数(当数的个数不少于3时)都分别成等差数列,若顶点A,B,C处的三个数互不相同且和为1,记所有顶点上的数之和为f(n),则有f(2)=2,求f(3)和f(n).
由下列各式:1>,1++>1,1++++++>,1+++……+>2,你能得出怎样的结论,并进行证明
下面玩掷骰子放球的游戏:若掷出1点,甲盒中放入一球;若掷出2点或是3点,乙盒中放入一球;若掷出4点或5点或6点,丙盒中放入一球.设掷n次后,甲、乙、丙盒内的球数分别为x,y,z.
(1)当n=3时,求x、y、z成等差数列的概率;
(2)当n=6时,求x、y、z成等比数列的概率;
(3)设掷4次后,甲盒和乙盒中球的个数差的绝对值为ξ,求Eξ.