(本小题满分16分)设数列{an}满足:a1=1,a2=2,an+2=(n≥1,n∈N* ).
).
(1) 求证:数列是常数列;
(2) 求证:当n≥2时,2<a-a≤3;
(3) 求a2 011的整数部分.
已知极坐标系的极点与直角坐标系的原点重合,极轴与直角坐标系的x轴的正半轴重合.设点O为坐标原点, 直线 (参数
(参数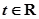 )与曲线
)与曲线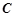 的极坐标方程为
的极坐标方程为 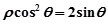
(1)求直线l与曲线C的普通方程;
(2)设直线l与曲线C相交于A,B两点,证明: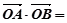 0.
0.
如图,AB是⊙O的直径,弦BD、CA的延长线相交于点E,EF垂直BA的延长线于点F. 求证:
(1) ;
;
(2)

已知函数f (x)=lnx,g(x)=ex.
(1)若函数φ (x) =" f" (x)- ,求函数φ (x)的单调区间;
,求函数φ (x)的单调区间;
(2)设直线l为函数的图象上一点A(x0,f (x0))处的切线.证明:在区间(1,+∞)上存在唯一的x0,使得直线l与曲线y=g(x)相切.
在直角坐标系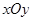 中,椭圆
中,椭圆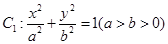 的左、右焦点分别为
的左、右焦点分别为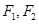 . 其中
. 其中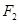 也是抛物线
也是抛物线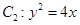 的焦点,点
的焦点,点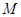 为
为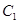 与
与 在第一象限的交点,且
在第一象限的交点,且
(1)求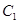 的方程;
的方程;
(2)若过点 的直线与
的直线与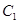 交于不同的两点
交于不同的两点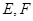 .
. 在
在 之间,试求
之间,试求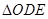 与
与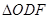 面积之比的取值范围.(O为坐标原点)
面积之比的取值范围.(O为坐标原点)
如图,棱柱ABCD—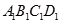 的所有棱长都为2,
的所有棱长都为2,  ,侧棱
,侧棱 与底面ABCD的所成角为60°,
与底面ABCD的所成角为60°, ⊥平面ABCD,
⊥平面ABCD, 为
为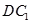 的中点.
的中点.
(1)证明:BD⊥ ;
;
(2)证明: 平面
平面 ;
;
(3)求二面角D

 C的余弦值.
C的余弦值.