如图,已知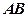
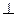 平面
平面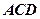 ,
,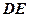 ∥
∥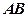 ,
,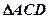 是正三角形,
是正三角形,
且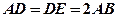 .
.
(1)设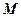 是线段
是线段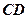 的中点,求证:
的中点,求证: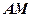 ∥平面
∥平面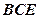 ;
;
(2)求直线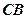 与平面
与平面 所成角的余弦值.
所成角的余弦值.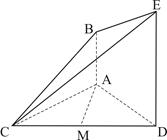
已知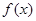 是二次函数,
是二次函数,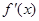 是它的导函数,且对任意的
是它的导函数,且对任意的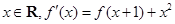 恒成立
恒成立
(Ⅰ)求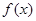 的解析式;
的解析式;
(Ⅱ)设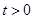 ,曲线
,曲线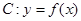 在点
在点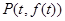 处的切线为
处的切线为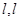 与坐标轴围成的三角形面积为
与坐标轴围成的三角形面积为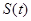 ,求
,求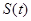 的最小值。
的最小值。
已知函数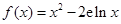 ,求函数
,求函数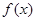 的单调区间和最值。
的单调区间和最值。
已知两定点F1(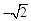 ,0),F2(
,0),F2(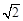 ,0)满足条件
,0)满足条件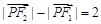 的点P的轨迹方程是曲线C,直线
的点P的轨迹方程是曲线C,直线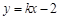 与曲线C交于A、B两点,且
与曲线C交于A、B两点,且 .
.
1、求曲线C的方程;
2、若曲线C上存在一点D,使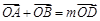 ,求m的值及点D到直线AB的距离.
,求m的值及点D到直线AB的距离.
如图,在四棱锥P—ABCD中,平面PAB⊥平面ABCD,底面ABCD是边长为2的正方形,△PAB是等边三角形.
1、求PC与平面ABCD所成角的正弦值;
2、求二面角B—AC—P的余弦值;
求点A到平面PCD的距离.
已知,以点C(t, )为圆心的圆与x轴交于O、A两点,与y轴交于O、B两点.
)为圆心的圆与x轴交于O、A两点,与y轴交于O、B两点.
1、求证:S△AOB为定值;
2、设直线 与圆C交于点M、N,若OM = ON,求圆C的方程.
与圆C交于点M、N,若OM = ON,求圆C的方程.