从8名运动员中选4人参加4×100米接力赛,在下列条件下,各有多少种不同的排法?(用数字结尾)
(1)甲、乙两人必须跑中间两棒;
(2)若甲、乙两人只有一人被选且不能跑中间两棒;
(3)若甲、乙两人都被选且必须跑相邻两棒.
某公司为了实现1000万元利润的目标,准备制定一个激励销售人员的奖励方案:在销售利润达到10万元时,按销售利润进行奖励,且奖金 (单位:万元)随销售利润
(单位:万元)随销售利润 (单位:万元)的增加而增加,但奖金总数不超过5万元,同时奖金不能超过利润的
(单位:万元)的增加而增加,但奖金总数不超过5万元,同时奖金不能超过利润的 %.现有三个奖励模型:
%.现有三个奖励模型: ,分析与推导哪个函数模型能符合该公司的要求?并给予证明.(注:
,分析与推导哪个函数模型能符合该公司的要求?并给予证明.(注: )
)
设函数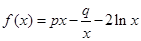 ,且
,且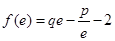 ,其中
,其中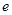 是自然对数的底数.
是自然对数的底数.
(1)求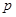 与
与 的关系;
的关系;
(2)若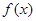 在其定义域内为单调函数,求
在其定义域内为单调函数,求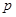 的取值范围.
的取值范围.
设 ,
,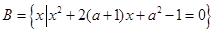 ,且B
,且B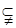 A,求实数
A,求实数 的取值范围.
的取值范围.
设函数 ,(
,( )
)
(I)求函数 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;
(Ⅱ)当 时,求
时,求 的最大值.
的最大值.
依法纳税是每个公民应尽的义务,国家征收个人工资、薪金所得税是分段计算的:总收入不超过2 000元的,免征个人工资、薪金所得税;超过2 000元部分需征税,设全月纳税所得额(所得额指工资、薪金中应纳税的部分)为x,x=全月总收入-2 000元,税率如表所示:
| 级数 |
全月应纳税所得额x |
税率 |
| 1 |
不超过500元部分 |
5% |
| 2 |
超过500元至2 000元部分 |
10% |
| 3 |
超过2 000元至5 000元部分 |
15% |
| … |
… |
… |
| 9 |
超过100 000元部分 |
45% |
(1)若应纳税额为f(x),试用分段函数表示1~3级纳税额f(x)的计算公式;
(2)某人2008年10月份工资总收入为4 200元,试计算这个人10月份应纳个人所得税多少元?