(本小题满分l2分)
已知函数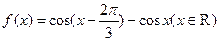 .
.
(Ⅰ)求函数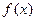 的最小正周期及单调递增区间;
的最小正周期及单调递增区间;
(Ⅱ)
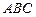 内角
内角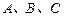 的对边长分别为
的对边长分别为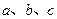 ,若
,若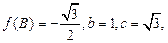 求
求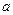 的值.
的值.
(本小题满分10分)选修4-1:几何证明选讲已知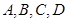 为圆
为圆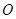 上的四点,直线
上的四点,直线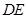 为圆
为圆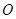 的切线,
的切线,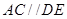 ,
,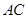 与
与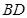 相交于
相交于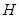 点.
点.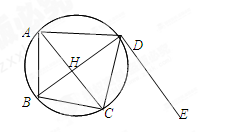
(Ⅰ)求证: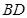 平分
平分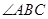 .
.
(Ⅱ)若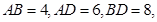 求
求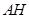 的长.
的长.
(本小题满分12分)已知函数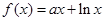 ,函数
,函数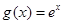 ,其中
,其中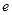 为自然对数的底数.
为自然对数的底数.
(Ⅰ)讨论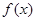 的单调性;
的单调性;
(Ⅱ)若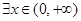 ,使得不等式
,使得不等式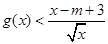 成立,试求实数
成立,试求实数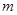 的取值范围;
的取值范围;
(Ⅲ)当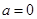 时,对于
时,对于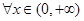 ,求证:
,求证: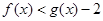 .
.
(本小题满分12分)已知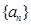 是公差为
是公差为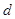 的等差数列,它的前
的等差数列,它的前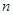 项和为
项和为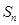 ,且
,且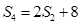 .
.
(Ⅰ)求公差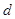 的值;
的值;
(Ⅱ)若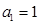 ,
,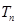 是数列
是数列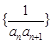 的前
的前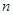 项和,不等式
项和,不等式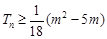 对所有的
对所有的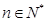 恒成立,求正整数
恒成立,求正整数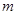 的最大值.
的最大值.
(本小题满分12分)已知函数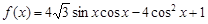 .
.
(Ⅰ)求函数 在
在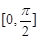 上的值域;
上的值域;
(Ⅱ)若对于任意的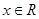 ,不等式
,不等式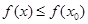 恒成立,求
恒成立,求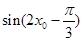 .
.
(本小题满分12分)已知集合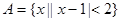 ,
,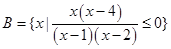 ,
,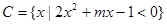 ,
,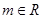 .
.
(Ⅰ)求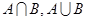 ;
;
(Ⅱ)若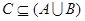 ,求
,求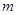 的取值范围.
的取值范围.