某中学的高二(1)班男同学有
名，女同学有
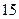名，老师按照分层抽样的方法组建了一个
人的课外兴趣小组．
（Ⅰ）求某同学被抽到的概率及课外兴趣小组中男、女同学的人数；
（Ⅱ）经过一个月的学习、讨论，这个兴趣小组决定选出两名同学做某项实验，方法是先从小组里选出
名同学做实验，该同学做完后，再从小组内剩下的同学中选一名同学做实验，求选出的两名同学中恰有一名女同学的概率；
（Ⅲ）试验结束后，第一次做试验的同学得到的试验数据为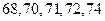
，第二次做试验的同学得到的试验数据为
，请问哪位同学的实验更稳定？并说明理由.
在四棱锥
中，
底面
，
，
，
，
，
是
的中点．
（1）证明：
；
（2）证明：
平面
；
（3）（限理科生做，文科生不做）求二面角
的余弦值．
已知命题
，命题
，若
是
的充分不必要条件，求实数
的取值范围．
已知函数
，
．
（1）求
的值；
（2）设
求
的值．
某省2015年全省高中男生身高统计调查数据显示：全省100000名男生的身高服从正态分布N（170．5，16）．现从我校高三年级男生中随机抽取50名测量身高，测量发现被测学生身高全部介于157．5cm和187．5 cm之间，将测量结果按如下方式分成6组：第一组 [157．5，162．5），第二组[162．5，167．5），…，第6 组[182．5，187．5]，下图是按上面分组方法得到的频率分布直方图．
（1）试评估我校高三年级男生在全省高中男生中的平均身高状况；
（2）求这50名男生身高在177．5cm以上（含177．5 cm）的人数；
（3）在这50名男生身高在177．5cm以上（含177．5cm）的人中任意抽取2人，该2人中身高排名（以高到低）在全省前130名的人数记为
，求的数学期望．
参考数据:若～
，则
，
，
某校学习小组开展“学生语文成绩与外语成绩的关系”的课题研究，对该校高三年级800名学生上学期期末语文和外语成绩，按优秀和不优秀分类得结果：语文和外语都优秀的有60人，语文成绩优秀但外语成绩不优秀的有140人，外语成绩优秀但语文成绩不优秀的有100人．
（1）能否在犯错概率不超过0．001的前提下认为该校学生的语文成绩和外语成绩有关系?
（2）将上述调查所得到的频率视为概率，从该校高三年级学生成绩中，有放回地随机抽取3名学生的成绩，记抽取的3个成绩中语文、外语两科成绩至少有一科优秀的个数为X，求X的分布列和期望．
 |
0．010 |
0．005 |
0．001 |
 |
6．635 |
7．789 |
10．828 |
