(本小题满分12分)如图是在竖直平面内的一个“通道游戏”.图中竖直线段和斜线段都表示通道,并且在交点处相遇,若竖直线段有第一条的为第一层,有二条的为第二层,……,依次类推.现有一颗小弹子从第一层的通道里向下运动.记小弹子落入第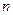 层第
层第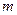 个竖直通道(从左至右)的概率为
个竖直通道(从左至右)的概率为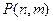 .(已知在通道的分叉处,小弹子以相同的概率落入每个通道)
.(已知在通道的分叉处,小弹子以相同的概率落入每个通道)
(Ⅰ)求 的值,并猜想
的值,并猜想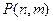 的表达式.(不必证明)
的表达式.(不必证明)
(Ⅱ)设小弹子落入第6层第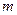 个竖直通道得到分数为
个竖直通道得到分数为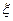 ,其中
,其中 ,试求
,试求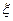 的分布列及数学期望.
的分布列及数学期望.
(本小题满分13分)已知函数 ,其中
,其中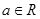 .
.
(1)当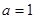 时,求函数的单调增区间。
时,求函数的单调增区间。
(2)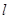 为
为 在
在 处的切线,且
处的切线,且 图像上的点都不在
图像上的点都不在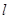 的上方,求
的上方,求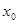 的取值范围.
的取值范围.
数列 满足
满足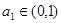 ,
,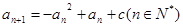
(1)证明:“对任意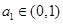 ,
,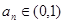 ”的充要条件是“
”的充要条件是“ ”
”
(2)若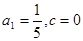 ,数列
,数列 满足
满足 ,设
,设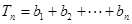 ,
,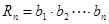 ,若对任意的
,若对任意的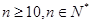 ,不等式
,不等式 的解集非空,求满足条件的实数
的解集非空,求满足条件的实数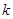 的最小值。
的最小值。
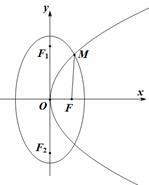
(本小题满分13分)如图,抛物线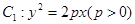 与椭圆
与椭圆 交于第一象限内一点
交于第一象限内一点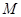 ,
, 为抛物线
为抛物线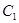 的焦点,
的焦点,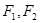 分别为椭圆
分别为椭圆 的上下焦点,已知
的上下焦点,已知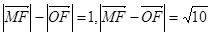
(1)求抛物线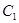 和椭圆
和椭圆 的方程;
的方程;
(2)是否存在经过M的直线 ,与抛物线和椭圆分别交于非M的两点
,与抛物线和椭圆分别交于非M的两点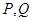 ,使得
,使得 ?若存在请求出直线的斜率,若不存在,请说明理由。
?若存在请求出直线的斜率,若不存在,请说明理由。
(本小题满分12分)如图1,在边长为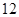 的正方形
的正方形 中,
中,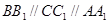 ,且
,且 ,且
,且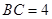 ,
, 分别交
分别交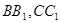 于点
于点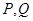 ,将该正方形沿
,将该正方形沿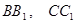 折叠,使得
折叠,使得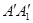 与
与 重合,构成图
重合,构成图 所示的三棱柱
所示的三棱柱 ,在图
,在图 中:
中:
(1)求证: ;
;
(2)在底边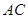 上有一点
上有一点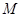 ,使得
,使得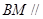 平面
平面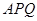 ,求点
,求点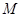 到平面
到平面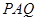 的距离.
的距离.
(本小题满分12分)甲、乙两人对弈棋局,甲胜、乙胜、和棋的概率都是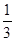 ,规定有一方累计2胜或者累计2和时,棋局结束。棋局结束时,若是累计两和的情形,则宣布甲乙都获得冠军;若一方累计2胜,则宣布该方获得冠军,另一方获得亚军。设结束时对弈的总局数为X.
,规定有一方累计2胜或者累计2和时,棋局结束。棋局结束时,若是累计两和的情形,则宣布甲乙都获得冠军;若一方累计2胜,则宣布该方获得冠军,另一方获得亚军。设结束时对弈的总局数为X.
(1)设事件A:“X=3且甲获得冠军”,求A的概率;
(2)求X的分布列和数学期望。