如图,在三棱柱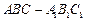 中,
中,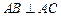 ,顶点
,顶点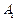 在底面
在底面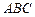 上的射影恰为点
上的射影恰为点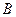 ,且
,且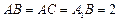 .
.
(Ⅰ)证明:平面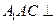 平面
平面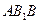 ;
;
(Ⅱ)求棱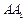 与
与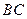 所成的角的大小;
所成的角的大小;
(Ⅲ)若点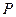 为
为 的中点,并求出二面角
的中点,并求出二面角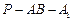 的平面角的余弦值.
的平面角的余弦值.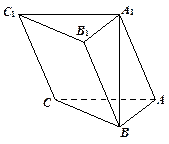
已知曲线C1的参数方程是 (φ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程是ρ=2,正方形ABCD的顶点都在C2上,且A,B,C,D依逆时针次序排列,点A的极坐标为
(φ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程是ρ=2,正方形ABCD的顶点都在C2上,且A,B,C,D依逆时针次序排列,点A的极坐标为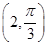 .
.
(1)求点A,B,C,D的直角坐标;
(2)设P为C1上任意一点,求|PA|2+|PB|2+|PC|2+|PD|2的取值范围.
在直角坐标系xOy.圆C1:x2+y2=4,圆C2:(x-2)2+y2=4.
(1)在以O为极点,x轴正半轴为极轴的极坐标系中,分别写出圆C1,C2的极坐标方程,并求出圆C1,C2的交点坐标(用极坐标表示);
(2)求圆C1与C2的公共弦的参数方程.
在直角坐标系 中以
中以 为极点,
为极点, 轴正半轴为极轴建立坐标系.圆
轴正半轴为极轴建立坐标系.圆 ,直线
,直线 的极坐标方程分别为
的极坐标方程分别为 .
.
(1)
(2)
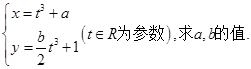
在直角坐标系中,以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系.已知点A的极坐标为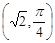 ,直线
,直线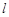 的极坐标方程为
的极坐标方程为 ,且点A在直线
,且点A在直线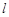 上。
上。
(1)求 的值及直线
的值及直线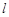 的直角坐标方程;
的直角坐标方程;
(2)圆C的参数方程为 ,试判断直线l与圆C的位置关系.
,试判断直线l与圆C的位置关系.
已知动点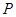 ,Q都在曲线C:
,Q都在曲线C: (β为参数)上,对应参数分别为β=α
(β为参数)上,对应参数分别为β=α
与α=2π(0<α<2π),M为PQ的中点。
(1)求M的轨迹的参数方程
(2)将M到坐标原点的距离d表示为 的函数,并判断M的轨迹是否过坐标原点。
的函数,并判断M的轨迹是否过坐标原点。