将一个半径适当的小球放入如图所示的容器最上方的入口处, 小球将自由下落.小球在下落过程中,将3次遇到黑色障碍物,最后落入A袋或B袋中.已知小球每次遇到黑色障碍物时向左、右两边下落的概率都是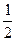 .
.
(Ⅰ)求小球落入A袋中的概率P(A);
(Ⅱ)在容器入口处依次放入4个小球,记X为落入A袋中小球的个数,试求X=3的概率和X的数学期望EX.
(本小题满分12分)设函数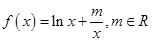 .
.
(Ⅰ)当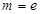 (
(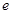 为自然对数的底数)时,求
为自然对数的底数)时,求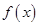 的极小值;
的极小值;
(Ⅱ)讨论函数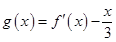 零点的个数;
零点的个数;
(Ⅲ)若对任意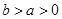 ,
,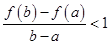 恒成立,求
恒成立,求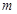 取值范围.
取值范围.
一个暗箱里放着6个黑球、4个白球.
(1)依次取出3个球,不放回,若第1次取出的是白球,求第3次取到黑球概率;
(2)有放回地依次取出3个球,若第1次取出的是白球,求第3次取到黑球概率;
(3)有放回地依次取出3个球,求取到白球个数 的分布列和期望.
的分布列和期望.
为考查某种药物预防疾病的效果,进行动物试验,得到如下丢失数据的列联表:
| 患病 |
未患病 |
总计 |
|
| 没服用药 |
20 |
30 |
50 |
| 服用药 |
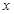 |
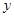 |
50 |
| 总计 |
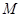 |
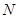 |
100 |
设从没服用药的动物中任取两只,未患病数为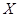 ;从服用药物的动物中任取两只,未患病数为
;从服用药物的动物中任取两只,未患病数为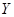 ,工作人员曾计算过
,工作人员曾计算过 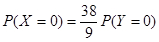
(1)求出列联表中数据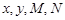 的值;
的值;
(2)能够以99%的把握认为药物有效吗?
参考公式: ,其中
,其中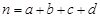 ;
;
①当K2≥3.841时有95%的把握认为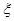 、
、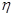 有关联;
有关联;
②当K2≥6.635时有99%的把握认为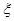 、
、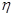 有关联.
有关联.
由四个不同的数字1,2,4,x组成无重复数字的三位数.
(1)若x=5,其中能被5整除的共有多少个?
(2)若x=9,其中能被3整除的共有多少个?
(3)若x=0,其中的偶数共有多少个?
(4)若所有这些三位数的各位数字之和是252,求x.
某校甲、乙两个班级各有5名编号为1,2,3,4,5的学生进行投篮训练,每人投10次,投中的次数统计如下表:
| 学生 |
1号 |
2号 |
3号 |
4号 |
5号 |
| 甲班 |
6 |
5 |
7 |
9 |
8 |
| 乙班 |
4 |
8 |
9 |
7 |
7 |
(1)从统计数据看,甲、乙两个班哪个班成绩更稳定(用数字特征说明);
(2)若把上表数据作为学生投篮命中率,规定两个班级的1号和2号同学分别代表自己的班级参加比赛,每人投篮一次,将甲、乙两个班两名同学投中的次数之和分别记作 和
和 ,试求
,试求 和
和 的分布列和数学期望.
的分布列和数学期望.