如图,已知正三棱柱 的底面正三角形的边长是2,D是
的底面正三角形的边长是2,D是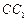 的中点,直线
的中点,直线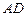 与侧面
与侧面 所成的角是
所成的角是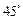 .
.
(Ⅰ)求二面角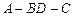 的大小;
的大小;
(Ⅱ)求点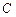 到平面
到平面 的距离.
的距离.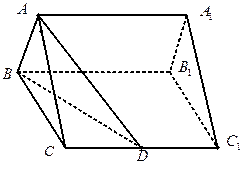
已知函数 的定义域为
的定义域为 ,若
,若 在
在 上为增函数,则称
上为增函数,则称 为“比增函数”;
为“比增函数”;
(Ⅰ)若函数 是“比增函数”,求实数
是“比增函数”,求实数 的取值范围;
的取值范围;
(Ⅱ)已知 ,
, 为“比增函数”,且
为“比增函数”,且 的部分函数值由下表给出,
的部分函数值由下表给出,
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
求证: .
.
)如图,AB为圆O的直径,点E、F在圆O上,AB∥EF,矩形ABCD所在的平面和圆O所在的平面互相垂直,且AB=2,AD=EF=1.
(Ⅰ)求证:平面DAF⊥平面CBF;
(Ⅱ)设FC的中点为M,求证:OM∥平面DAF;
(Ⅲ)设平面CBF将几何体EFABCD分成的两个锥体的体积分别为 ,求
,求 .
.
△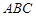 中,角
中,角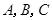 的对边分别为
的对边分别为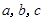 ,且
,且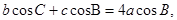
(Ⅰ)求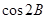 ;
;
(Ⅱ)若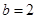 且
且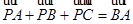 ,求△
,求△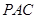 面积最大值.
面积最大值.
设数列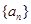 的前n项和为
的前n项和为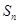 ,满足
,满足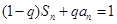 ,且
,且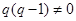 .
.
(Ⅰ)求证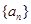 是等比数列;
是等比数列;
(Ⅱ)若存在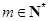 使得
使得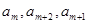 成等差数列,求
成等差数列,求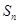 .
.
在平面直角坐标系 中,已知
中,已知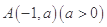 ,
,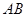 是圆
是圆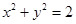 的一条直径,
的一条直径,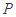 是动点,且直线
是动点,且直线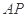 与
与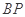 的斜率之积等于
的斜率之积等于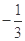 .
.
(1)求动点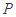 的轨迹方程;
的轨迹方程;
(2)设直线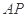 和
和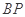 分别与直线
分别与直线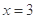 交于点
交于点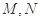 ,问:是否存在点
,问:是否存在点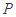 使得
使得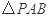 与
与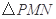 的面积相等?若存在,求出点
的面积相等?若存在,求出点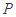 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.