已知平面内一动点
到点
(1,0)的距离与点
到
轴的距离的等等于1.
(1)求动点
的轨迹 的方程;
的方程;
(2)过点
作两条斜率存在且互相垂直的直线
,设
与轨迹
相交于点
,
与轨迹
相交于点
,求
的最小值.
三人独立破译同一份密码.已知三人各自破译出密码的概率分别为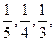 且他们是否破译出密码互不影响.
且他们是否破译出密码互不影响.
(Ⅰ)求恰有二人破译出密码的概率;
(Ⅱ)“密码被破译”与“密码未被破译”的概率哪个大?说明理由.
已知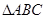 的三个内角
的三个内角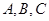 所对的边分别为
所对的边分别为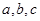 ,
,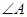 是锐角,且
是锐角,且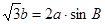 .
.
(Ⅰ)求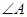 的度数;
的度数;
(Ⅱ)若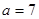 ,
,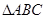 的面积为
的面积为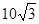 ,求
,求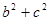 的值.
的值.
(本小题共14分)
数列 的前n项和为
的前n项和为 ,点
,点 在直线
在直线
上.
(I)求证:数列 是等差数列;
是等差数列;
(II)若数列 满足
满足 ,求数列
,求数列 的前n项和
的前n项和
(III)设 ,求证:
,求证:
(本小题共14分)
已知椭圆的中点在原点O,焦点在x轴上,点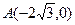 是其左顶点,点C在椭圆上且
是其左顶点,点C在椭圆上且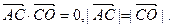
(I)求椭圆的方程;
(II)若平行于CO的直线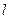 和椭圆交于M,N两个不同点,求
和椭圆交于M,N两个不同点,求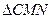 面积的最大值,并求此时直线
面积的最大值,并求此时直线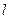 的方程.
的方程.
(本小题共13分)
已知函数
(I)若x=1为 的极值点,求a的值;
的极值点,求a的值;
(II)若 的图象在点(1,
的图象在点(1, )处的切线方程为
)处的切线方程为 ,求
,求 在区间[-2,4]上的最大值;
在区间[-2,4]上的最大值;
(III)当 时,若
时,若 在区间(-1,1)上不单调,求a的取值范围.
在区间(-1,1)上不单调,求a的取值范围.