以下茎叶图记录了甲、乙两组各四名同学的植树棵数。乙组记录中有一个数据模糊,无法确认,在图中经
表示.

(Ⅰ)如果
,求乙组同学植树棵数的平均数和方差;
(Ⅱ)如果
,分别从甲、乙两组中随机选取一名同学,求这两名同学的植树总棵数为19的概率.
(注:方差
,其中
为
的平均数)
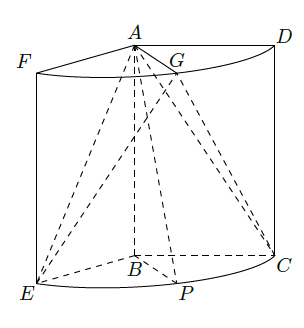
如图,几何体是圆柱的一部分,它是由矩形ABCD(及其内部)以AB边所在直线为旋转轴旋转120°得到的,G是 的中点.
(Ⅰ)设P是 上的一点,且 ,求 的大小;
(Ⅱ)当 , 时,求二面角 的大小.
设函数 ,其中 ,已知 .
(Ⅰ)求 ;
(Ⅱ)将函数 的图象上各点的横坐标伸长为原来的2倍(纵坐标不变),再将得到的图象向左平移 个单位,得到函数 的图象,求 在 上的最小值.
[选修4-5:不等式选讲]已知函数
.
(1)求不等式 的解集;
(2)若不等式 的解集非空,求实数 m的取值范围.
[选修4―4:坐标系与参数方程]
在直角坐标系 xOy中,直线
 的参数方程为
( t为参数),直线
的参数方程为
.设 l 1与 l 2的交点为 P,当 k变化时, P的轨迹为曲线 C .
的参数方程为
( t为参数),直线
的参数方程为
.设 l 1与 l 2的交点为 P,当 k变化时, P的轨迹为曲线 C .
(1)写出 C的普通方程;
(2)以坐标原点为极点, x轴正半轴为极轴建立极坐标系,设 , M为 l 3与 C的交点,求 M的极径.
已知函数
x.
(1)讨论 的单调性;
(2)当 时,证明 .