我市某镇的一种特产由于运输原因，长期只能在当地销售．当地政府-优题课

我市某镇的一种特产由于运输原因，长期只能在当地销售．当地政府对
该特产的销售投资收益为：每投入x万元，可获得利润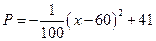（万元）．当
地政府拟在“十二•五”规划中加快开发该特产的销售，其规划方案为：在规划前后对该项
目每年最多可投入100万元的销售投资，在实施规划5年的前两年中，每年都从100万元中
拨出50万元用于修建一条公路，两年修成，通车前该特产只能在当地销售；公路通车后的
3年中，该特产既在本地销售，也在外地销售．在外地销售的投资收益为：每投入x万元，
可获利润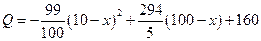（万元）
⑴若不进行开发，求5年所获利润的最大值是多少？
⑵若按规划实施，求5年所获利润（扣除修路后）的最大值是多少？
⑶根据⑴、⑵，该方案是否具有实施价值？

科目数学题型解答题难度中等

知识点：二次函数在给定区间上的最值

在一个箱内装入只有标号不同的三颗小球，标号分别为1，2，3．每次随机取出一颗小球，记下标号作为得分，再将小球放回箱内．小明现已取球三次，得分分别为1分，3分，2分，小明又从箱内取球两次，若五次得分的平均数不小于2.2分，请用画树状图或列表的方法，求发生“五次取球得分的平均数不小于2.2分”情况的概率．

列方程解应用题：

小明和小刚约定周末到某体育公园打羽毛球．他们两家到体育公园的距离分别是1200米，3000米，小刚骑自行车的速度是小明步行速度的3倍，若二人同时到达，则小明需提前4分钟出发，求小明和小刚两人的速度．

如图，四边形 $ABCD$ 是正方形， $ΔEFC$ 是等腰直角三角形，点 $E$ 在 $AB$ 上，且 $∠ CEF = 90 °$ ， $FG ⊥ AD$ ，垂足为点 $G$ ．

（1）试判断 $AG$ 与 $FG$ 是否相等？并给出证明；

（2）若点 $H$ 为 $CF$ 的中点， $GH$ 与 $DH$ 垂直吗？若垂直，给出证明；若不垂直，说明理由．

若二次函数 $y = a x^{2} + bx + c$ 的图象与 $x$ 轴、 $y$ 轴分别交于点 $A (3, 0)$ 、 $B (0, - 2)$ ，且过点 $C (2, - 2)$ ．

（1）求二次函数表达式；

（2）若点 $P$ 为抛物线上第一象限内的点，且 $S_{ΔPBA} = 4$ ，求点 $P$ 的坐标；

（3）在抛物线上 $(AB$ 下方）是否存在点 $M$ ，使 $∠ ABO = ∠ ABM$ ？若存在，求出点 $M$ 到 $y$ 轴的距离；若不存在，请说明理由．

在矩形 $ABCD$ 中， $AE ⊥ BD$ 于点 $E$ ，点 $P$ 是边 $AD$ 上一点．

（1）若 $BP$ 平分 $∠ ABD$ ，交 $AE$ 于点 $G$ ， $PF ⊥ BD$ 于点 $F$ ，如图①，证明四边形 $AGFP$ 是菱形；

（2）若 $PE ⊥ EC$ ，如图②，求证： $AE \cdot AB = DE \cdot AP$ ；

（3）在（2）的条件下，若 $AB = 1$ ， $BC = 2$ ，求 $AP$ 的长．

试卷网试题网古诗词网作文网范文网