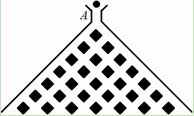
（本小题满分12分）如图，在竖直平面内有一个“游戏滑道”，空白部分表示光滑滑道，黑色正方形表示障碍物，自上而下第一行有1个障碍物，第二行有2个障碍物，……，依次类推．一个半径适当的光滑均匀小球从入口A投入滑道，小球将自由下落，已知小球每次遇到正方形障碍物上顶点时，向左、右两边下落的概率都是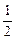
．记小球遇到第
行第
个障碍物（从左至右）上顶点的概率为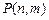
．
（Ⅰ）求
，
的值，并猜想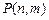的表达式（不必证明）；
（Ⅱ）已知
，设小球遇到第6行第个障碍物（从左至右）上顶点时，
得到的分数为
，试求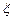
的分布列及数学期望．
时，求
在
上的最值；
在区间
上不单调．求实数
的取值范围．
，底面
为菱形，
平面
，
分别是
的中点．
；
,求二面角
的余弦值．
中，内角
的对边分别为
，面积为
，已知
．
的值；
，
，求
．
是偶函数，且
在
上单调递增．
，求
的定义域和值域．
的部分图象如图所示．
的解析式；