请考生在（22）、（23）、（24）三题中任选一题作答，如果多答，则按做的第一题记分．作答时用2B铅笔在答题卡上把所选题目对应题号右侧的方框涂黑．
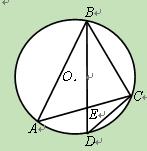
（22）（本小题满分10分）选修4—1：几何证明选讲。如图，⊙O是△
的外接圆，D
是的中点，BD交AC于E．
（Ⅰ）求证：CD
=DE·DB；
（Ⅱ）若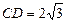
，O到AC的距离为1，求⊙O的半径
．
（Ⅰ）当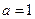
时，证明函数
只有一个零点；
（Ⅱ）若函数在区间
上是减函数，求实数
的取值范围
（1）求证：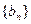
是等差数列；
（2）求数列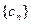
的前n项和Sn；
（3）若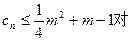
一切正整数n恒成立，求实数m的取值范围
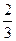
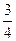
（1）设
为攻关期满时获奖的攻关小组数，求的分布列及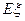
；
（2）设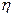
为攻关期满时获奖的攻关小组数与没有获奖的攻关小组数之差的平方，记“函数
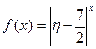在定义域内单调递减”为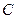事件
，求事件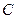的概率
侧棱PA=PD＝
，底面ABCD为直角梯形，其中
BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点.
（1）求证：PO⊥平面ABCD；
（2）求异面直线PB与CD所成角的余弦值；
（3）线段AD上是否存在点Q，使得它到平面PCD的距离为
？若存在，求出
的值；若不存在，请说明理由.
数列{an}的前n项和记为Sn，
（1）求{an}的通项公式;
（2）等差数列{bn}的各项为正，其前n项和为Tn，且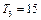
，又
成等比数列，求Tn