(本小题满分14分)
已知椭圆G与双曲线 有相同的焦点,且过点
有相同的焦点,且过点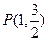
(1)求椭圆G的方程
(2)设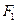 、
、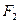 是椭圆G的左焦点和右焦点,过
是椭圆G的左焦点和右焦点,过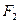 的直线
的直线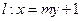 与椭圆G相交于A、B两点,请问
与椭圆G相交于A、B两点,请问 的内切圆M的面积是否存在最大值?若存在,求出这个最大值及直线
的内切圆M的面积是否存在最大值?若存在,求出这个最大值及直线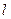 的方程,若不存在,请说明理由
的方程,若不存在,请说明理由
已知函数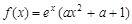
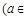 R).
R).
(Ⅰ)若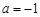 ,求曲线
,求曲线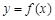 在点
在点 处的的切线方程;
处的的切线方程;
(Ⅱ)若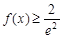 对任意
对任意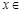
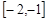 恒成立,求实数
恒成立,求实数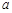 的取值范围.
的取值范围.
已知椭圆 (a>b>0)的焦距为4,且与椭圆
(a>b>0)的焦距为4,且与椭圆 有相同的离心率,斜率为
有相同的离心率,斜率为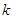 的直线
的直线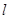 经过点
经过点 (0,1),与椭圆
(0,1),与椭圆 交于不同两点
交于不同两点 、
、 .
.
(1)求椭圆 的标准方程;
的标准方程;
(2)当椭圆 的右焦点
的右焦点 在以
在以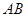 为直径的圆内时,求
为直径的圆内时,求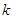 的取值范围.
的取值范围.
三棱柱 中,侧棱与底面垂直,
中,侧棱与底面垂直,  ,
,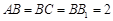 ,
, 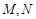 分别是
分别是 ,
, 的中点.
的中点.
(Ⅰ)求证: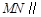 平面
平面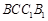 ;
;
(Ⅱ)求证: 平面
平面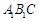 ;
;
(Ⅲ)求三棱锥
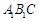 的体积.
的体积.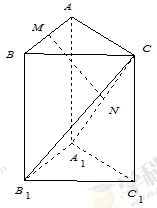
已知函数f(x)=ax-1-ln x(a∈R).
(1)讨论函数f(x)的单调性;
(2)若函数f(x)在x=1处取得极值,不等式f(x)≥bx-2对∀x∈(0,+∞)恒成立,求实数b的取值范围;
(3)当x>y>e-1时,证明不等式exln(1+y)>eyln(1+x).
已知抛物线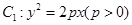 的焦点
的焦点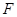 以及椭圆
以及椭圆 的上、下焦点及左、右顶点均在圆
的上、下焦点及左、右顶点均在圆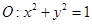 上.
上.
(1)求抛物线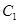 和椭圆
和椭圆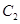 的标准方程;
的标准方程;
(2)过点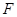 的直线交抛物线
的直线交抛物线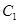 于
于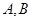 两不同点,交
两不同点,交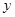 轴于点
轴于点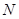 ,已知
,已知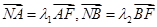 ,求
,求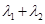 的值;
的值;
(3)直线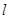 交椭圆
交椭圆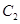 于
于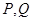 两不同点,
两不同点,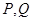 在
在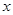 轴的射影分别为
轴的射影分别为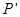 、
、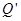 ,
,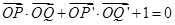 ,若点
,若点 满足
满足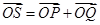 ,证明:点
,证明:点 在椭圆
在椭圆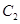 上.
上.