(本小题满分14分 )已知函数
)已知函数 (a为常数)
(a为常数)
(1)当 时,分析函数
时,分析函数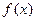 的单调性;
的单调性;
(2)当a >0时,试讨论曲线 与
与 轴的公共点的个数。
轴的公共点的个数。
设正项数列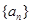 的前
的前 项和为
项和为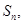 且
且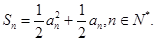 正项等比数列满足:
正项等比数列满足: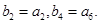
(1)求数列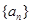 、
、 的通项公式;
的通项公式;
(2)设 数列
数列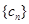 的前
的前 项和为
项和为 求所有正整数
求所有正整数 的值,使得
的值,使得 恰好为数列
恰好为数列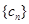 中的项.
中的项.
如图,已知椭圆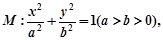 其率心率为
其率心率为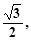 两条准线之间的距离为
两条准线之间的距离为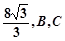 分别为椭圆
分别为椭圆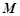 的上、下顶点,过点
的上、下顶点,过点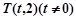 的直线
的直线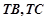 分别与椭圆
分别与椭圆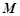 交于
交于 两点.
两点.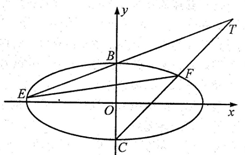
(1)椭圆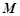 的标准方程;
的标准方程;
(2)若△ 的面积是△
的面积是△ 的面积的
的面积的 倍,求
倍,求 的最大值.
的最大值.
如图,在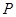 地正西方向
地正西方向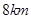 的
的 处和正东方向
处和正东方向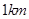 的
的 处各一条正北方向的公路
处各一条正北方向的公路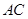 和
和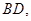 现计划在
现计划在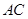 和
和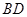 路边各修建一个物流中心
路边各修建一个物流中心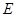 和
和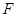 .为缓解交通压力,决定修建两条互相垂直的公路
.为缓解交通压力,决定修建两条互相垂直的公路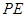 和
和 设
设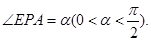
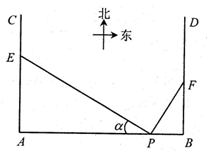
(1)为减少周边区域的影响,试确定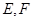 的位置,使△
的位置,使△ 与△
与△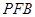 的面积之和最小;
的面积之和最小;
(2)为节省建设成本,试确定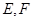 的位置,使
的位置,使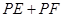 的值最小.
的值最小.
如图,矩形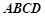 所在平面与三角形
所在平面与三角形 所在平面相交于
所在平面相交于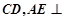 平面
平面
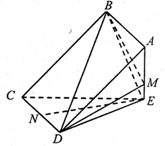
(1)求证: 平面
平面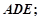
(2)若点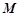 在线段
在线段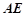 上,
上,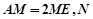 为线段
为线段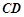 中点,求证:
中点,求证: 平面
平面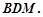
在△ ,角
,角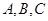 的对边分别为
的对边分别为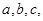 已知
已知
(1)求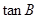 的值;
的值;
(2)若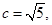 求△
求△ 的面积.
的面积.