(9分)某中学学生为了解该校学生喜欢球类活动的情况,随机抽取了若干名学生进行问卷调查(要求每位学生只能填写一种自己喜欢的球类),并将调查的结果绘制成如下的两幅不完整的统计图.

请根据图中提供的信息,解答下面的问题:
(1)参加调查的学生共有 人,在扇形图中,表示“其他球类”的扇形的圆心角为 度;
(2)将条形图补充完整;
(3)若该校有2000名学生,则估计喜欢“篮球”的学生共有 人.
如图,在△ABC中,∠ACB=90°,∠B>∠A,点D为边AB的中点,DE∥BC交AC于点E,CF∥AB交DE的延长线于点F.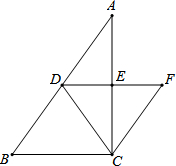

(1)求证:DE=EF;
(2)连接CD,过点D作DC的垂线交CF的延长线于点G,求证:∠B=∠A+∠DGC.
四边形ABCD为矩形,G是BC上的任意一点,DE⊥AG于点E.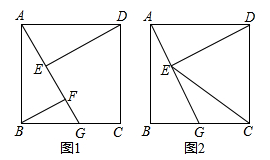
(1)如图1,若AB=BC,BF∥DE,且交AG于点F,求证:AF-BF=EF;
(2)如图2,在(1)条件下,AG=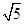 BG,求
BG,求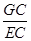 ;
;
如图,ABCD是正方形,BE∥AC,AE=AC,CF∥AE,求证:∠AEB=2∠BCF。
如图,菱形 中,
中, ,
,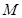 是
是 的中点,
的中点, 是对角线
是对角线 上的一个动点,若
上的一个动点,若 的最小值是
的最小值是 ,求
,求 的长。
的长。
如图,在▱ABCD中,BC=2AB,点M是AD的中点,CF⊥AB于F,如果∠AFM=50°,求∠B的度数.