(11·西宁)(本小题满分8分)如图15,阅读对话,解答问题.
盒子中有三个除数字外完全相同的小球—1,1,2.
小兵:我蒙上眼睛,先从盒子中摸出一个小球(摸出后不放回),用P表示我摸出小球上标有的数字.
小红:你摸出后,我也蒙上眼睛,再从盒子中摸出一个小球,用Q表示我摸出小球上标有的数字.
(1)试用树形图或列表法写出满足关于x的方程x2+px+q=0的所有等可能结果;
(2)求(1)中方程有实数根的概率.
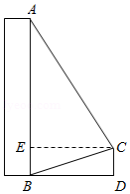
如图,四边形 是正方形,点 是射线 上的动点,连接 ,以 为对角线作正方形 , , , 按逆时针排列),连接 , .
(1)当点 在线段 上时.
①求证: ;
②求证: ;
(2)设正方形 的面积为 ,正方形 的面积为 ,以 , , , 为顶点的四边形的面积为 ,当 时,请直接写出 的值.

某服装厂生产 品种服装,每件成本为71元,零售商到此服装厂一次性批发 品牌服装 件时,批发单价为 元, 与 之间满足如图所示的函数关系,其中批发件数 为10的正整数倍.
(1)当 时, 与 的函数关系式为 .
(2)某零售商到此服装厂一次性批发 品牌服装200件,需要支付多少元?
(3)零售商到此服装厂一次性批发 品牌服装 件,服装厂的利润为 元,问: 为何值时, 最大?最大值是多少?

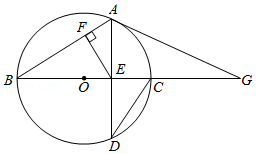
如图, 是 的直径, 是 的弦, 交 于点 ,连接 , ,过点 作 ,垂足为 , .
(1)求证: ;
(2)点 在 的延长线上,连接 , .
①求证: 与 相切;
②当 , 时,直接写出 的长.
如图,某数学活动小组要测量建筑物 的高度,他们借助测角仪和皮尺进行了实地测量,测量结果如下表.
|
测量项目 |
测量数据 |
|
测角仪到地面的距离 |
|
|
点 到建筑物的距离 |
|
|
从 处观测建筑物顶部 的仰角 |
|
|
从 处观测建筑物底部 的俯角 |
|
请根据需要,从上面表格中选择3个测量数据,并利用你选择的数据计算出建筑物 的高度.(结果精确到0.1米,参考数据: , , . , , (选择一种方法解答即可)
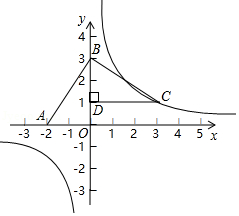
如图, 、 两点的坐标分别为 , ,将线段 绕点 逆时针旋转 得到线段 ,过点 作 ,垂足为 ,反比例函数 的图象经过点 .
(1)直接写出点 的坐标,并求反比例函数的解析式;
(2)点 在反比例函数 的图象上,当 的面积为3时,求点 的坐标.