三、解答题（本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤）。
17、（本小题满分10分）某校从参加高一年级期中考试的学生中随机抽取60名学生，将其数学成绩(均为整数)分成六段[40, 50)，[50, 60)，…，[90, 100] 后得到如下部分频率分布直方图．观察图形的信息，回答下列问题：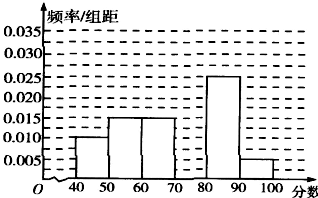
（I）求分数在 [70，80)内的频率，并补全这个频率分布直方图；
（Ⅱ）统计方法中，同一组数据常用该组区间的中点值作为代表，据此估计本次考试的平均分；
(Ⅲ) 根据频率分布直方图估计这次高一年级期中考试的学生成绩的中位数(保留整数)。
（本小题满分10分）已知定义域为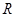
的函数
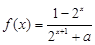是奇函数．
（1）求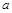
的值；
（2）若对任意的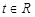
，不等式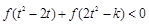
恒成立，求实数
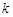的取值范围．
（本小题满分10分）如图是总体的一个样本频率分布直方图，且在[15，18
内频数为8．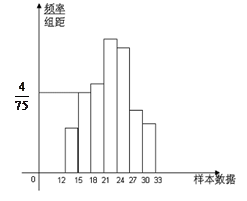
（1）求样本在[15，18内的频率；
（2）求样本容量；
（3）若在[12，15内的小矩形面积为0.06，求在[18，33内的频数．
对任意
，函数
的值恒大于零，求
的取值范围．
某学校校办工厂有毁坏的房屋一座，留有一面14m的旧墙，现准备利用这面墙的一段为面墙，建造平面图形为矩形且面积为126
的厂房（不管墙高），工程的造价是：
（1）修1m旧墙的费用是造1m新墙费用的25%;
（2）拆去1m旧墙用所得的材料来建1m新墙的费用是建1m新墙费用的50%.问如何利用旧墙才能使建墙的费用最低？
解关于x的不等式