（本小题满分12分）有这样一则公益广告:人们在享受汽车带来的-优题课

题文

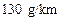（本小题满分12分）有这样一则公益广告:“人们在享受汽车带来的便捷与舒适的同时，却不得不呼吸汽车排放的尾气”，汽车已是城市中碳排放量比较大的行业之一．某市为响应国家节能减排，更好地保护环境，决定将于年起取消排放量超过的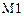型新车挂牌．检测单位对目前该市保有量最大的甲类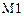型品牌车随机抽取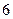辆进行了排放量检测，记录如下（单位：）.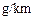

(Ⅰ)已知，求的值及样本标准差；
（Ⅱ）从被检测的甲类品牌车中任取2辆，则至少有一辆不符合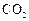排放量的概率是多少？

科目数学题型解答题难度中等

登录免费查看答案和解析

相关试题

为了解学生身高情况，某校以 $10 %$ 的比例对全校 $700$ 名学生按性别进行分层抽样检查，测得身高情况的统计图如下：

（Ⅰ）估计该校男生的人数；
（Ⅱ）估计该校学生身高在 $170 ~ 185 c m$ 之间的概率；
（Ⅲ）从样本中身高在 $180 ~ 190 c m$ 之间的男生中任选 $2$ 人，求至少有 $1$ 人身高在 $185 ~ 190 c m$ 之间的概率.

如图，在四棱锥 $P - A B C D$ 中，底面 $A B C D$ 是矩形， $P A ⊥$ 平面 $A B C D$ ， $A P = A B$ ， $B P = B C = 2$ ， $E, F$ 分别是 $P B, P C$ 的中点.
(Ⅰ)证明： $E F / /$ 平面 $P A D$ ；
(Ⅱ)求三棱锥 $E - A B C$ 的体积 $V$ .

在 $△ A B C$ 中，已知 $B = 45^{°}$ , $D$ 是 $B C$ 边上的一点， $A D = 10, A C = 14, D C = 6$ ，求 $A B$ 的长.

已知 ${a_{n}}$ 是公差不为零的等差数列， $a_{1} = 1$ ，且 $a_{1}, a_{3}, a_{9}$ 成等比数列.
（Ⅰ）求数列 ${a_{n}}$ 的通项;

（Ⅱ）求数列 ${2^{a_{n}}}$ 的前 $n$ 项和 $S_{n}$ .

已知抛物线 $C : y^{2} = 4 x$ 的焦点为 $F$ ，过点 $K (- 1, 0)$ 的直线 $l$ 与 $C$ 相交于 $A$ 、 $B$ 两点，点 $A$ 关于 $x$ 轴的对称点为 $D$ .
（Ⅰ）证明：点 $F$ 在直线 $B D$ 上；
（Ⅱ）设 $\overset{⇀}{F A} \cdot \overset{⇀}{F B} = \frac{8}{9}$ ，求 $△ B D K$ 的内切圆 $M$ 的方程 .

试卷网试题网古诗词网作文网范文网

Copyright ©2020-2025 优题课 youtike.com 版权所有

粤ICP备20024846号