若复数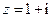 ,求实数
,求实数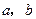 使
使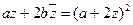 成立.(其中
成立.(其中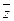 为
为 的共轭复数)
的共轭复数)
已知: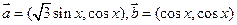 ,
,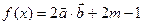 (
( ).(Ⅰ) 求
).(Ⅰ) 求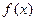 关于
关于 的表达式,并求
的表达式,并求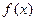 的最小正周期;(Ⅱ) 若
的最小正周期;(Ⅱ) 若 时,
时,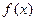 的最小值为5,求
的最小值为5,求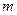 的值.
的值.
( 12分)近段时间我国北方严重缺水, 某城市曾一度取消洗车行业. 时间久了,车容影响了市容市貌. 今年该市决定引进一种高科技产品污水净化器,允许洗车行开始营业,规定洗车行必须购买这种污水净化器,使用净化后的污水(达到生活用水标准)洗车. 污水净化器的价格是每台90万元,全市统一洗车价格为每辆每次8元. 该市今年的汽车总量是80000辆,预计今后每年汽车数量将增加2000辆.洗车行A经过测算,如果全市的汽车总量是x,那么一年内在该洗车行洗车的平均辆次是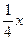 ,该洗车行每年的其他费用是20000元. 问:洗车行A从今年开始至少经过多少年才能收回购买净化器的成本?(注:洗车行A买一台污水净化器就能满足洗车净水需求)
,该洗车行每年的其他费用是20000元. 问:洗车行A从今年开始至少经过多少年才能收回购买净化器的成本?(注:洗车行A买一台污水净化器就能满足洗车净水需求)
(本小题满分13分) 如图,四边形ABCD是边长为1的正方形,
如图,四边形ABCD是边长为1的正方形,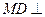 平面ABCD,
平面ABCD,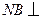 平面
平面 ,且
,且 ,E为BC的中点.(Ⅰ)求异面直线NE与AM所成角的余弦值;(Ⅱ)在线段AN上是否存在点S,使得ES
,E为BC的中点.(Ⅰ)求异面直线NE与AM所成角的余弦值;(Ⅱ)在线段AN上是否存在点S,使得ES 平面AMN?若存在,求线段AS的长;若不存在,请说明理由.
平面AMN?若存在,求线段AS的长;若不存在,请说明理由.
在△ABC中,角A、B、C的对边分别为a、b、c,且满足(2a-c)cosB=bcosC.
(Ⅰ)求角B的大小;(Ⅱ)设
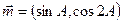 ,
,

 的最大值是5,求k的值.
的最大值是5,求k的值.
(本小题满分12分)已知函数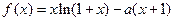 ,其中
,其中 为常数.
为常数.
(1)当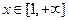 时,
时, 恒成立,求
恒成立,求 的取值范围;(2)求
的取值范围;(2)求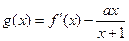 的单调区间.
的单调区间.