知识背景：恩施来凤有一处野生古杨梅群落，其野生杨梅是一种具特-优题课

知识背景：恩施来凤有一处野生古杨梅群落，其野生杨梅是一种具特殊价值的绿色食品．在当地市场出售时，基地要求“杨梅”用双层上盖的长方体纸箱封装（上盖纸板面积刚好等于底面面积的2倍，如图）
（1）实际运用：如果要求纸箱的高为0.5米，底面是黄金矩形（宽与长的比是黄金比，取黄金比为0.6），体积为0.3立方米．
①按方案1（如图）做一个纸箱，需要矩形硬纸板A₁B₁C₁D₁的面积是多少平方米？
②小明认为，如果从节省材料的角度考虑，采用方案2（如图）的菱形硬纸板A₂B₂C₂D₂做一个纸箱比方案1更优，你认为呢？请说明理由．
（2）拓展思维：北方一家水果商打算在基地购进一批“野生杨梅”，但他感觉（1）中的纸箱体积太大，搬运吃力，要求将纸箱的底面周长、底面面积和高都设计为原来的一半，你认为水果商的要求能办到吗？请利用函数图象验证．

科目数学题型解答题难度中等

知识点：应用类问题

国家规定“中小学生每天在校体育活动时间不低于 $1 h$ ”．为此，某市就“每天在校体育活动时间”的问题随机调查了辖区内部分初中学生，根据调查结果绘制成的统计图（部分）如图所示，其中分组情况是：

$A$ 组： $t < 0.5 h$

$B$ 组： $0.5 h ⩽ t < 1 h$

$C$ 组： $1 h ⩽ t < 1.5 h$

$D$ 组： $t ⩾ 1.5 h$

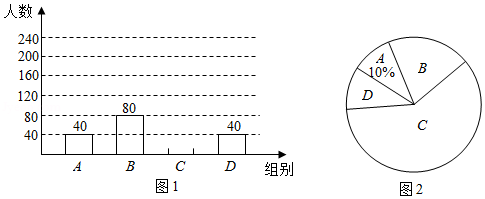
请根据上述信息解答下列问题：

（1）本次调查的人数是　　人；

（2）请根据题中的信息补全频数分布直方图；

（3） $D$ 组对应扇形的圆心角为　　 $°$ ；

（4）本次调查数据的中位数落在　　组内；

（5）若该市辖区约有80000名初中学生，请估计其中达到国家规定体育活动时间的学生人数约有多少．

如图，在 $ΔABC$ 中， $∠ B = 40 °$ ， $∠ C = 50 °$ ．

（1）通过观察尺规作图的痕迹，可以发现直线 $DF$ 是线段 $AB$ 的　　，射线 $AE$ 是 $∠ DAC$ 的　　；

（2）在（1）所作的图中，求 $∠ DAE$ 的度数．

解不等式组 $\{\begin{matrix} x - 3 (x - 2) ⩾ 4 \\ \frac{2 x - 1}{3} ⩽ \frac{x + 1}{2} \end{matrix}$ ．

先化简，再求值： $\frac{2}{x^{2} - 1} \div \frac{1}{x + 1} - \frac{1}{x - 1}$ ，从1，2，3这三个数中选择一个你认为适合的 $x$ 代入求值．

如图，直线 $y = \frac{1}{2} x + 1$ 与 $x$ ， $y$ 轴分别交于点 $B$ ， $A$ ，顶点为 $P$ 的抛物线 $y = a x^{2} - 2 ax + c$ 过点 $A$ ．

（1）求出点 $A$ ， $B$ 的坐标及 $c$ 的值；

（2）若函数 $y = a x^{2} - 2 ax + c$ 在 $3 ⩽ x ⩽ 4$ 时有最大值为 $a + 2$ ，求 $a$ 的值；

（3）连接 $AP$ ，过点 $A$ 作 $AP$ 的垂线交 $x$ 轴于点 $M$ ．设 $ΔBMP$ 的面积为 $S$ ．

①直接写出 $S$ 关于 $a$ 的函数关系式及 $a$ 的取值范围；

②结合 $S$ 与 $a$ 的函数图象，直接写出 $S > \frac{1}{8}$ 时 $a$ 的取值范围．