（本小题满分12分）
已知数列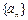
中，
（1）求数列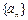的通项公式；
（2）设
，若对任意的正整数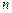
，当
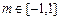时，不等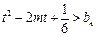
恒成立，求实数
的取值范围.
必做题, 本小题10分．解答时应写出文字说明、证明过程或演算步骤．
已知等式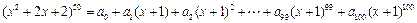
，其中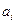
（
=0，1，2，…，100）为实常数．求：
（1）
的值；（2）
的值．
必做题, 本小题10分．解答时应写出文字说明、证明过程或演算步骤．
如图，在底面边长为1，侧棱长为2的正四棱柱
中，P是侧棱
上的一点，
.
（1）当
时，求直线AP与平面BDD1B1所成角的度数；
（2）在线段
上是否存在一个定点
，使得对任意的m，
⊥AP，并证明你的结论. 
选修4－5：不等式证明选讲
已知函数
. 若不等式
对a¹0, a、bÎR恒成立，求实数x的范围.
C. 选修4－4：坐标系与参数方程.
已知在直角坐标系x0y内，直线l的参数方程为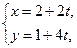
(t为参数)．以Ox为极轴建立极坐标系，圆C的极坐标方程为
.
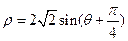(1)写出直线l的普通方程和圆C的直角坐标方程；
(2)判断直线l和圆C的位置关系.
B. 选修4－2：矩阵与变换
已知
, 求矩阵B.