(本小题满分14分)
已知函数
(1) 当 时,求函数
时,求函数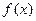 的最小值;
的最小值;
(2) 求函数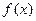 的单调区间;
的单调区间;
(3) 试说明是否存在实数 使
使 的图象与
的图象与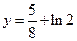 无公共点.
无公共点.
已知函数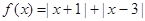 .
.
(Ⅰ)求不等式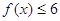 的解集;
的解集;
(Ⅱ)若关于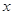 的不等式
的不等式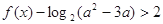 恒成立,求实数
恒成立,求实数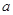 的取值范围.
的取值范围.
在直角坐标系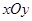 中,半圆C的参数方程为
中,半圆C的参数方程为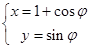 (
( 为参数,
为参数,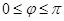 ),以O为极点,x轴的非负半轴为极轴建立极坐标系.
),以O为极点,x轴的非负半轴为极轴建立极坐标系.
(Ⅰ)求C的极坐标方程;
(Ⅱ)直线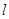 的极坐标方程是
的极坐标方程是 ,射线OM:
,射线OM: 与半圆C的交点为O、P,与直线
与半圆C的交点为O、P,与直线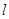 的交点为Q,求线段PQ的长.
的交点为Q,求线段PQ的长.
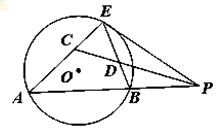
如图,已知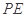 切⊙
切⊙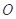 于点
于点 ,割线
,割线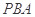 交⊙
交⊙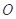 于
于 两点,∠
两点,∠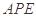 的平分线和
的平分线和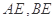 分别交于点
分别交于点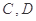 .
.
求证:(1)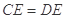 ;
;
(2)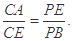
设函数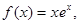
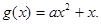 [K]
[K]
(1)若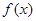 与
与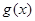 具有完全相同的单调区间,求
具有完全相同的单调区间,求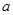 的值;
的值;
(2)若当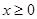 时恒有
时恒有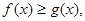 求
求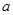 的取值范围.
的取值范围.
已知椭圆
 的焦距为
的焦距为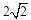 ,且过点
,且过点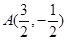 .
.
(1)求椭圆的方程;
(2)已知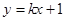 ,是否存在
,是否存在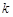 使得点
使得点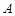 关于
关于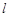 的对称点
的对称点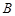 (不同于点
(不同于点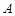 )在椭圆
)在椭圆 上?若存在求出此时直线
上?若存在求出此时直线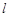 的方程,若不存在说明理由.
的方程,若不存在说明理由.