已知二项式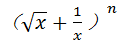 的展开式中各项系数的和为64.
的展开式中各项系数的和为64.
(I)求n;
(II)求展开式中的常数项.
本小题满分14分
已知:数列 ,
,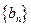 中,
中, ,
, ,且当
,且当 时,
时,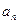 ,
, ,
,
 成等差数列,
成等差数列, ,
, ,
,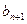 成等比数列.
成等比数列.
(1)求数 列
列 ,
,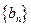 的通项公式;
的通项公式;
(2)求最小自然数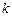 ,使得当
,使得当 时,对任意实数
时,对任意实数
 ,不等式
,不等式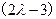
 ≥
≥
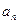
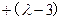 恒成立;
恒成立;
(3)设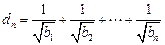 (
( ),求证:当
),求证:当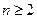 都有
都有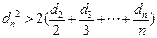 .
.
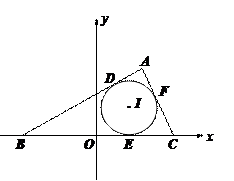
本小题满分12分 的内切圆与三边
的内切圆与三边 的切点分别为
的切点分别为 ,已知
,已知 ,内切圆圆心
,内切圆圆心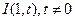 ,设点
,设点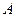 的轨迹为
的轨迹为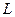 .
.
(1)求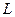 的方程;
的方程;
(2)过点 的动直线
的动直线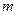 交曲线
交曲线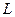 于不同的两点
于不同的两点 (点
(点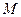 在
在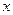 轴的上方),问在
轴的上方),问在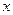 轴上是否存在一定点
轴上是否存在一定点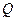 (
(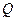 不与
不与 重合),使
重合),使 恒成立,若存在,试求出
恒成立,若存在,试求出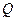 点的坐标;若不存在,说明理由.
点的坐标;若不存在,说明理由.
(本小题满分12分)
在斜三棱柱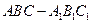 中,
中,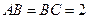 ,
,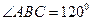 ,又顶点
,又顶点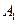 在底面
在底面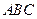 上的射影落在
上的射影落在 上,侧棱
上,侧棱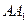 与底面
与底面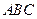 成
成 角,
角, 为
为 的中点.
的中点.
(1)求证: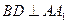 ;
;
(2)如果二面角 为直二面角,试求侧棱
为直二面角,试求侧棱 与侧面
与侧面 的距离.
的距离.
(本小题满分12 分)
分)
定义在 上的函数
上的函数 ,其中
,其中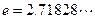 是自然对数的底数,
是自然对数的底数,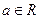 .
.
(1) 若函数 在点
在点 处连续,求
处连续,求 的值;
的值;
(2) 若函数 为
为 上的单调函数,求实
上的单调函数,求实 数
数 的取值范围,并判断此时函数
的取值范围,并判断此时函数 在
在 上是否为单调函数.
上是否为单调函数.
(本小题满分12分)
某学校要用鲜花布置花圃中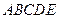 五个不同区域,要求同一区域上用同一种颜色的鲜花,相邻区域使用不同颜色的鲜花.现有红、黄、蓝、白、紫五种不同颜色的鲜花可供任意选择.
五个不同区域,要求同一区域上用同一种颜色的鲜花,相邻区域使用不同颜色的鲜花.现有红、黄、蓝、白、紫五种不同颜色的鲜花可供任意选择.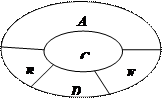
(1)当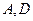 区域同时用红色鲜花时,求布置花圃的不同方法的种数;
区域同时用红色鲜花时,求布置花圃的不同方法的种数;
(2)求恰 有两个区域用红色鲜花的概率;
有两个区域用红色鲜花的概率;
(3)记 为花圃中用红色鲜花布置的区域的个数,求随机变量
为花圃中用红色鲜花布置的区域的个数,求随机变量 的分布列及其数学期望
的分布列及其数学期望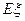 .
.