某商店以6元/千克的价格购进某种干果1140千克,并对其进行筛选分成甲级干果与乙级干果后同时开始销售。这批干果销售结束后,店主从销售统计中发出:甲级干果与乙级干果在销售过程中每天都有销量,且在同一天卖完;甲级干果从开始销售至销售的第 天的总销量
天的总销量 (千克)与
(千克)与 的关系为
的关系为 ;乙级干果从开始销售至销售的第
;乙级干果从开始销售至销售的第 天的总销量
天的总销量 (千克)与
(千克)与 的关系为
的关系为 ,且乙级干果的前三天的销售量的情况见下表:
,且乙级干果的前三天的销售量的情况见下表:
(1)求 、
、 的值;
的值;
(2)若甲级干果与乙级干果分别以8元/千克的6元/千克的零售价出售,则卖完这批干果获得的毛利润是多少元?
(3)问从第几天起乙级干果每天的销量比甲级干果每天的销量至少多6千克?
(说明:毛利润=销售总金额-进货总金额。这批干果进货至卖完的过程中的损耗忽略不计)
函数
(1)a=0时,求f(x)最小值;
(2)若f(x)在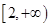 是单调减函数,求a的取值范围.
是单调减函数,求a的取值范围.
已知甲盒内有大小相同的1个红球和3个黑球, 乙盒内有大小相同的2个红球和4个黑球,现从甲、乙两个盒内各任取2个球.
(1)求取出的4个球均为黑球的概率;
(2)求取出的4个球中恰有1个红球的概率;
(3)设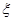 为取出的4个球中红球的个数,求
为取出的4个球中红球的个数,求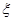 的分布列和数学期望
的分布列和数学期望
从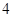 名男生和
名男生和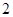 名女生中任选
名女生中任选 人参加演讲比赛,
人参加演讲比赛,
①求所选 人都是男生的概率;
人都是男生的概率;
②求所选 人恰有
人恰有 名女生的概率;
名女生的概率;
③求所选 人中至少有
人中至少有 名女生的概率.
名女生的概率.
(1)用反证法证明:在一个三角形中,至少有一个内角大于或等于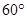 ;
;
(2)已知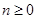 ,试用分析法证明:
,试用分析法证明: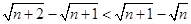 .
.
已知函数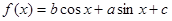 .
.
(1)当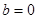 时,求
时,求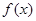 的值域;
的值域;
(2)当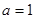 ,
,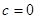 时,函数
时,函数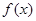 的图象关于
的图象关于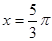 对称,求函数
对称,求函数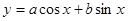 的对称轴;
的对称轴;
(3)若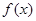 图象上有一个最低点
图象上有一个最低点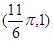 ,如果图象上每点纵坐标不变,横坐标缩短到原来的
,如果图象上每点纵坐标不变,横坐标缩短到原来的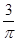 倍,然后向左平移1个单位可得
倍,然后向左平移1个单位可得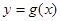 的图象,又知
的图象,又知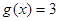 的所有正根从小到大依次为
的所有正根从小到大依次为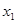 ,
,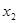 ,…
,…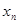 ,…且
,…且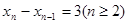 ,求
,求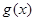 的解析式.
的解析式.