设函数 ,
,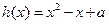 .
.
(Ⅰ)当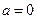 时,
时,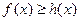 在
在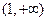 上恒成立,求实数
上恒成立,求实数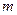 的取值范围;
的取值范围;
(Ⅱ)当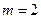 时
时 ,若函数
,若函数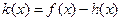 在
在 上恰有两个不同零点,求实数
上恰有两个不同零点,求实数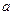 的取值范围;
的取值范围;
(Ⅲ)是否存在实数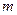 ,使函数
,使函数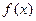 和函数
和函数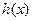 在公共定义域上具有相同的单调性?若存在,求出
在公共定义域上具有相同的单调性?若存在,求出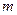 的值,若不存在,说明理由。
的值,若不存在,说明理由。
(理科)椭圆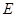 中心在原点
中心在原点 ,焦点在
,焦点在 轴上,其离心率
轴上,其离心率 ,过点
,过点 的直线
的直线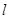 与椭圆
与椭圆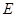 相交于
相交于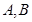 两点,且C分有向线段
两点,且C分有向线段 的比为2.
的比为2.
(1)用直线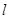 的斜率
的斜率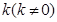 表示
表示 的面积;
的面积;
(2)当 的面积最大时,求椭圆E的方程.
的面积最大时,求椭圆E的方程.
(理科)如图,已知⊙ :
: 及点
及点
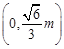 ,在⊙
,在⊙ 上任取一点
上任取一点 ′,连
′,连
 ′,并作
′,并作
 ′的中垂线l,设l与
′的中垂线l,设l与
 ′交于点P, 若点
′交于点P, 若点 ′取遍⊙
′取遍⊙ 上的点.
上的点.
(1)求点P的轨迹C的方程;
(2)设直线 与轨迹C相交于A、B两个不同的点,与x轴相交于点D.若
与轨迹C相交于A、B两个不同的点,与x轴相交于点D.若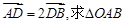 的面积取得最大值时的椭圆方程.
的面积取得最大值时的椭圆方程.
(文科)已知椭圆 的左、右两个顶点分别为A,B,直线
的左、右两个顶点分别为A,B,直线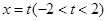 与椭圆相交于M,N两点,经过三点A,M,N的圆与经过三点B,M,N的圆分别记为圆C1与圆C2.
与椭圆相交于M,N两点,经过三点A,M,N的圆与经过三点B,M,N的圆分别记为圆C1与圆C2.
(1)求证:无论t如何变化,圆C1与圆C2的圆心距是定值;
(2)当t变化时,求圆C1与圆C2的面积的和S的最小值.
(理科)已知椭圆的中心在坐标原点O,焦点在x轴上,椭圆的短轴端点和焦点所组成的四边形为正方形,两准线间的距离为4。
(Ⅰ)求椭圆的方程;
(Ⅱ)直线 过点P(0,2)且与椭圆相交于A、B两点,当ΔAOB面积取得最大值时,求直线l的方程。
过点P(0,2)且与椭圆相交于A、B两点,当ΔAOB面积取得最大值时,求直线l的方程。
(文科)
|
已知椭圆 :
: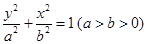 的右顶点为
的右顶点为 ,过
,过 的焦点且垂直长轴的弦长为
的焦点且垂直长轴的弦长为 .
.

 的方程;
的方程;
 在抛物线
在抛物线 :
: 上,
上, 在点
在点 处的切线与
处的切线与 交于点
交于点 .当线段
.当线段 的中点与
的中点与 的中点的横坐标相等时,求
的中点的横坐标相等时,求 的最小值.
的最小值.