(本小题满分12分) 甲、乙两人在一场五局三胜制的象棋比赛中,规定甲或乙无论谁先赢满三局就获胜,并且比赛就此结束.现已知甲、乙两人每比赛一局甲取胜的概率是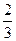 ,乙取胜的概率为
,乙取胜的概率为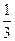 ,且每局比赛的胜负是独立的,试求下列问题:
,且每局比赛的胜负是独立的,试求下列问题:
(Ⅰ)比赛以甲3胜1而结束的概率;
(Ⅱ)比赛以乙3胜2而结束的概率;
(Ⅲ)设甲获胜的概率为a,乙获胜的概率为b,求a:b的值.
定义域为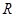 的奇函数
的奇函数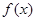 满足
满足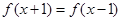 ,且当
,且当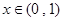 时,
时,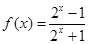 .
.
(Ⅰ)求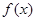 在
在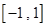 上的解析式;
上的解析式;
(Ⅱ)若存在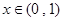 ,满足
,满足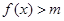 ,求实数
,求实数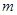 的取值范围.
的取值范围.
已知向量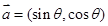 与
与 ,其中
,其中
(Ⅰ)若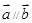 ,求
,求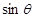 和
和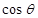 的值;
的值;
(Ⅱ)若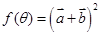 ,求
,求 的值域.
的值域.
设函数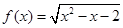 的定义域为集合
的定义域为集合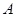 ,函数
,函数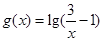 的定义域为集合
的定义域为集合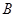 ,已知
,已知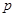 :
: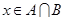 ;
;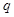 :
: 满足
满足 ,且若
,且若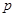 则
则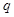 为真命题,求实数
为真命题,求实数 的取值范围.
的取值范围.
已知函数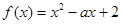 ,
, (
(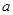 为常数)
为常数)
(1)当 时
时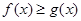 恒成立,求实数
恒成立,求实数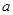 的取值范围;
的取值范围;
(2)若函数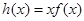 有对称中心为A(1,0),求证:函数
有对称中心为A(1,0),求证:函数 的切线
的切线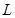 在切点处穿过
在切点处穿过 图象的充要条件是
图象的充要条件是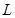 恰为函数在点A处的切线.(直线穿过曲线是指:直线与曲线有交点,且在交点左右附近曲线在直线异侧)
恰为函数在点A处的切线.(直线穿过曲线是指:直线与曲线有交点,且在交点左右附近曲线在直线异侧)
已知二次函数 与
与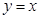 交于
交于 两点且
两点且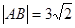 ,奇函数
,奇函数 ,当
,当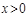 时,
时,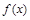 与
与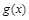 都在
都在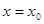 取到最小值.
取到最小值.
(1)求 的解析式;
的解析式;
(2)若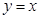 与
与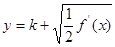 图象恰有两个不同的交点,求实数
图象恰有两个不同的交点,求实数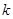 的取值范围.
的取值范围.