已知向量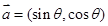 与
与 ,其中
,其中
(Ⅰ)若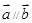 ,求
,求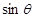 和
和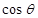 的值;
的值;
(Ⅱ)若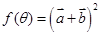 ,求
,求 的值域.
的值域.
(本小题满分13分)若 =
= ,
, =
= ,其中
,其中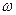 >0,记函数f(x)=(
>0,记函数f(x)=( +
+ )·
)· +k.
+k.
(1)若f(x)图象中相邻两条对称轴间的距离不小于 ,求
,求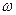 的取值范围.
的取值范围.
(2)若f(x)的最小正周期为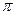 ,且当x
,且当x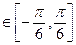 时,f(x)的最大值是
时,f(x)的最大值是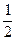 ,求f(x)的解析式,
,求f(x)的解析式,
(本小题满分13分)已知实数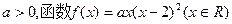 有极大值32.
有极大值32.
(1)求函数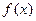 的单调区间;(2)求实数
的单调区间;(2)求实数 的值.
的值.
(本小题满分13分)已知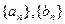 均为等差数列,且
均为等差数列,且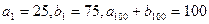 ,求数列
,求数列 的前100项之和。
的前100项之和。
(本小题满分14分) 已知函数 在
在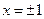 处取得极值。
处取得极值。
(Ⅰ)求函数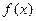 的解析式;
的解析式;
(Ⅱ)求证:对于区间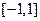 上任意两个自变量的值
上任意两个自变量的值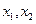 ,都有
,都有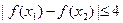 ;
;
(Ⅲ)若过点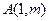 可作曲线
可作曲线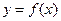 的
的 三条切线,求实数
三条切线,求实数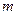 的取值范围。
的取值范围。
(本小题满分13分)已知函数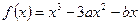 ,其中
,其中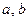 为实数.
为实数.
(Ⅰ) 若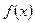 在
在 处取得的极值为
处取得的极值为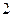 ,求
,求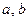 的值;
的值;
(Ⅱ)若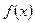 在区间
在区间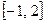 上为减函数,且
上为减函数,且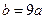 ,求
,求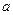 的取值范围.
的取值范围.