(本小题满分14分)
已知二次函数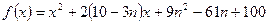 ,其中
,其中 .
.
(1)设函数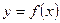 的图象的顶点的横坐标
的图象的顶点的横坐标 构成数列
构成数列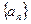 ,求证:数列
,求证:数列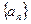 为等差数
为等差数 列;
列;
(2)设函数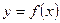 的图象的顶点到
的图象的顶点到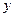 轴的距离构成数列
轴的距离构成数列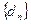 ,求数列
,求数列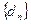 的前
的前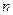 项和
项和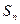 .
.
如图,A,B,C,D四点在同一圆上, 与
与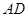 的延长线交于点
的延长线交于点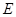 ,点
,点 在
在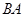 的延长线上.
的延长线上.
(Ⅰ)若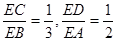 ,求
,求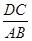 的值;
的值;
(Ⅱ)若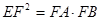 ,证明:
,证明: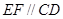 .
.
设函数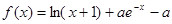 ,
,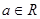 .
.
(Ⅰ)当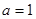 时,证明
时,证明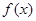 在
在 是增函数;
是增函数;
(Ⅱ)若 ,
,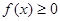 ,求
,求 的取值范围.
的取值范围.
如图椭圆 的右顶点是
的右顶点是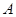 ,上下两个顶点分别为
,上下两个顶点分别为 ,四边形
,四边形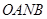 是矩形(
是矩形( 为原点),点
为原点),点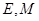 分别为线段
分别为线段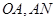 的中点.
的中点.
(Ⅰ)证明:直线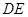 与直线
与直线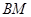 的交点在椭圆
的交点在椭圆 上;
上;
(Ⅱ)若过点 的直线交椭圆于
的直线交椭圆于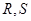 两点,
两点,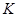 为
为 关于
关于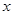 轴的对称点(
轴的对称点( 不共线),问:直线
不共线),问:直线 是否经过
是否经过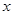 轴上一定点,如果是,求这个定点的坐标,如果不是,说明理由.
轴上一定点,如果是,求这个定点的坐标,如果不是,说明理由.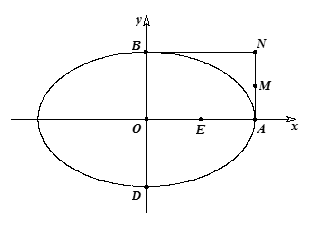
现有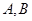 两个项目,投资
两个项目,投资 项目
项目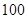 万元,一年后获得的利润为随机变量
万元,一年后获得的利润为随机变量 (万元),根据市场分析,
(万元),根据市场分析, 的分布列为:
的分布列为:
| X1 |
12 |
11.8 |
11.7 |
| P |
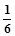 |
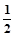 |
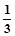 |
投资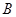 项目
项目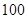 万元,一年后获得的利润
万元,一年后获得的利润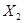 (万元)与
(万元)与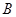 项目产品价格的调整(价格上调或下调)有关, 已知
项目产品价格的调整(价格上调或下调)有关, 已知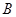 项目产品价格在一年内进行
项目产品价格在一年内进行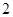 次独立的调整,且在每次调整中价格下调的概率都是
次独立的调整,且在每次调整中价格下调的概率都是 .
.
经专家测算评估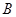 项目产品价格的下调与一年后获得相应利润的关系如下表:
项目产品价格的下调与一年后获得相应利润的关系如下表:
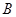 项目产品价格一年内下调次数 项目产品价格一年内下调次数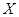 (次) (次) |
 |
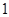 |
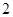 |
投资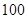 万元一年后获得的利润 万元一年后获得的利润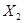 (万元) (万元) |
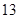 |
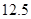 |
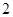 |
(Ⅰ)求 的方差
的方差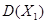 ;
;
(Ⅱ)求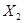 的分布列;
的分布列;
(Ⅲ)若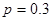 ,根据投资获得利润的差异,你愿意选择投资哪个项目?
,根据投资获得利润的差异,你愿意选择投资哪个项目?
(参考数据: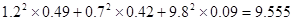 ).
).
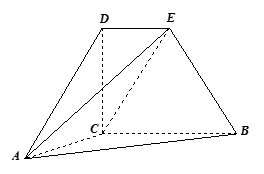
如图,四边形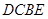 为直角梯形,
为直角梯形,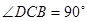 ,
,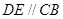 ,
,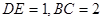 ,又
,又 ,
,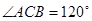 ,
,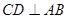 ,直线
,直线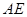 与直线
与直线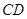 所成角为
所成角为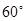 .
.
(Ⅰ)求证:平面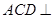 平面
平面 ;
;
(Ⅱ)求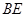 与平面
与平面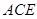 所成角的正弦值.
所成角的正弦值.