现有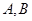 两个项目,投资
两个项目,投资 项目
项目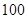 万元,一年后获得的利润为随机变量
万元,一年后获得的利润为随机变量 (万元),根据市场分析,
(万元),根据市场分析, 的分布列为:
的分布列为:
| X1 |
12 |
11.8 |
11.7 |
| P |
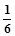 |
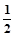 |
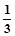 |
投资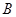 项目
项目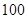 万元,一年后获得的利润
万元,一年后获得的利润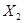 (万元)与
(万元)与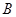 项目产品价格的调整(价格上调或下调)有关, 已知
项目产品价格的调整(价格上调或下调)有关, 已知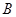 项目产品价格在一年内进行
项目产品价格在一年内进行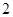 次独立的调整,且在每次调整中价格下调的概率都是
次独立的调整,且在每次调整中价格下调的概率都是 .
.
经专家测算评估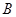 项目产品价格的下调与一年后获得相应利润的关系如下表:
项目产品价格的下调与一年后获得相应利润的关系如下表:
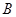 项目产品价格一年内下调次数 项目产品价格一年内下调次数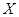 (次) (次) |
 |
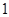 |
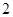 |
投资 万元一年后获得的利润 万元一年后获得的利润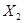 (万元) (万元) |
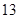 |
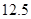 |
 |
(Ⅰ)求 的方差
的方差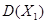 ;
;
(Ⅱ)求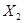 的分布列;
的分布列;
(Ⅲ)若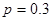 ,根据投资获得利润的差异,你愿意选择投资哪个项目?
,根据投资获得利润的差异,你愿意选择投资哪个项目?
(参考数据: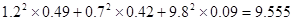 ).
).
(本小题满分12分)已知2件次品和3件正品混放在一起,现需要通过检测将其区分,
每次随机检测一件产品,检测后不放回,直到检测出2件次品或者检测出3件正品时检测
结束.
(1)求第一次检测出的是次品且第二次检测出的是正品的概率;
(2)己知每检测一件产品需要费用1 00元,设X表示直到检测出2件次品或者检测
出3件正品时所需要的检测费用(单位:元),求X的分布列和均值(数学期望).
(本小题满分10分)己知关于x的不等式|x+a|<b的解集为{x|2<x<4)
(1)求实数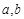 的值;
的值;
(2)求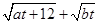 的最大值.
的最大值.
(本小题满分10分)在直角坐标系xOy中,曲线C1 (t为参数,t≠0),
(t为参数,t≠0),
其中0≤ <π,在以O为极点, x轴正半轴为极轴的极坐标系中,曲线
<π,在以O为极点, x轴正半轴为极轴的极坐标系中,曲线
C2 :  ,C3 :
,C3 : 
(1)求C2与C3交点的直角坐标;
(2)若C1与C2相交于点A,C1与C3相交于点B,求|AB|的最大值.
(本小题满分10分)选修4—5:不等式选讲
已知 .
.
(1)关于 的不等式
的不等式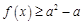 恒成立,求实数
恒成立,求实数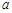 的取值范围;
的取值范围;
(2)设 ,且
,且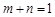 ,求证:
,求证: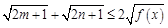 .
.
(本小题满分10分)选修4—4:极坐标与参数方程
在直角坐标系 中,直线
中,直线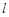 的参数方程为
的参数方程为 (
(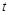 为参数).再以原点为极点,以
为参数).再以原点为极点,以 正半轴为极轴建立极坐标系,并使得它与直角坐标系
正半轴为极轴建立极坐标系,并使得它与直角坐标系 有相同的长度单位.在该极坐标系中圆
有相同的长度单位.在该极坐标系中圆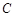 的方程为
的方程为 .
.
(1)求圆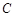 的直角坐标方程;
的直角坐标方程;
(2)设圆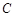 与直线
与直线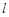 交于点
交于点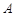 、
、 ,若点
,若点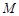 的坐标为
的坐标为 ,求
,求 的值.
的值.