如图椭圆 的右顶点是
的右顶点是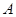 ,上下两个顶点分别为
,上下两个顶点分别为 ,四边形
,四边形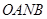 是矩形(
是矩形( 为原点),点
为原点),点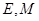 分别为线段
分别为线段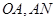 的中点.
的中点.
(Ⅰ)证明:直线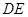 与直线
与直线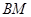 的交点在椭圆
的交点在椭圆 上;
上;
(Ⅱ)若过点 的直线交椭圆于
的直线交椭圆于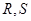 两点,
两点,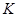 为
为 关于
关于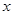 轴的对称点(
轴的对称点(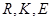 不共线),问:直线
不共线),问:直线 是否经过
是否经过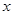 轴上一定点,如果是,求这个定点的坐标,如果不是,说明理由.
轴上一定点,如果是,求这个定点的坐标,如果不是,说明理由.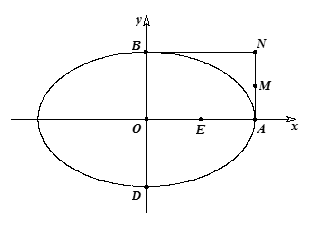
已知数列 的前n项和为
的前n项和为 ,且
,且
 ,
,
(1)求数列 的通项公式;
的通项公式;
(2)令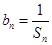 ,且数列
,且数列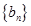 的前n项和为
的前n项和为 ,求
,求 ;
;
(3)若数列 满足条件:
满足条件: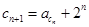 ,又
,又 ,是否存在实数
,是否存在实数 ,使得数列
,使得数列 为等差数列?
为等差数列?
宜昌市是全国11个重要旅游城市之一,促使了当地的宾馆生意火爆。当地某居民有楼房一幢,室内面积共180 ,拟分隔成两类房间作为旅游客房,大房间每间面积为18
,拟分隔成两类房间作为旅游客房,大房间每间面积为18 ,可住游客5名,每名游客每天住宿费为40元,小房间每间面积为15
,可住游客5名,每名游客每天住宿费为40元,小房间每间面积为15 ,可住游客3名,每名游客每天住宿费为50元,装修大房间每间需要1000元,装修小房间每间需要600元,如果他们只能筹8000元用于装修,且游客能住满客房,它应隔出大房间和小房间各多少间,能获最大利益?
,可住游客3名,每名游客每天住宿费为50元,装修大房间每间需要1000元,装修小房间每间需要600元,如果他们只能筹8000元用于装修,且游客能住满客房,它应隔出大房间和小房间各多少间,能获最大利益?

(1)求函数f(x)的最大值及取得最大值时相应的x的值;
(2)若函数y=f(2x)-a在区间 上恰有两个零点
上恰有两个零点 ,求tan(
,求tan( )的值
)的值
已知正数等比数列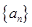 ,其中
,其中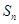 为
为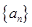 的前n项和,
的前n项和,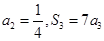 .
.
(1)求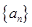 的通项公式;
的通项公式;
(2)若数列 满足
满足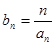 ,求
,求 的前n项和
的前n项和
已知△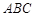 的三个内角
的三个内角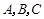 所对的边分别为a,b,c,向量
所对的边分别为a,b,c,向量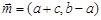 ,
,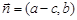 ,且
,且 .
.
(Ⅰ)求角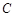 的大小;
的大小;
(Ⅱ)若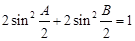 ,判断△
,判断△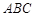 的形状.
的形状.