(本小题满分14分)
如图6,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,EF⊥PB交PB于点F.
(Ⅰ) 若PD=DC=2求三棱锥A-BDE的体积;
(Ⅱ) 证明PA∥平面EDB;
(Ⅲ) 证明PB⊥平面EFD.
选修4-1:几何证明选讲
如图,直线AB为圆的切线,切点为B,点C在圆上,锐角∠ABC的平分线BE交圆于点E,DB垂直BE交圆于D.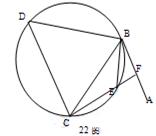
(Ⅰ)证明:DB=DC;
(Ⅱ)设圆的半径为1,BC=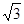 ,延长CE交AB于点F,求△BCF外接圆的半径.
,延长CE交AB于点F,求△BCF外接圆的半径.
已知函数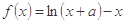 有且只有一个零点,其中a>0.
有且只有一个零点,其中a>0.
(Ⅰ)求a的值;
(Ⅱ)若对任意的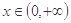 ,有
,有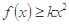 成立,求实数k的最大值;
成立,求实数k的最大值;
(Ⅲ)设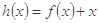 ,对任意
,对任意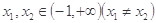 ,证明:不等式
,证明:不等式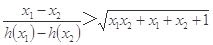 恒成立.
恒成立.
中心在坐标原点 ,焦点在坐标轴上的椭圆
,焦点在坐标轴上的椭圆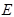 经过两点
经过两点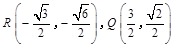 .分别过椭圆
.分别过椭圆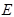 的焦点
的焦点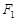 、
、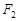 的动直线
的动直线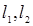 相交于
相交于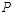 点,与椭圆
点,与椭圆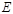 分别交于
分别交于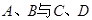 不同四点,直线
不同四点,直线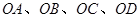 的斜率
的斜率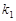 、
、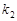 、
、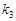 、
、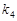 满足
满足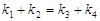 .
.
(1)求椭圆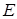 的方程;
的方程;
(2)是否存在定点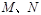 ,使得
,使得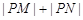 为定值.若存在,求出
为定值.若存在,求出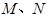 点坐标并求出此定值,若不存在,说明理由.
点坐标并求出此定值,若不存在,说明理由.
我市在夜明珠与黄柏河交汇形成的平湖水面上修建”三峡游轮中心”.其中有小型游艇出租给游客游玩,收费标准如下:租用时间不超过2小时收费100,超过2小时的部分按每小时100收取(不足一小时按一小时计算).现甲、乙两人独立来该景点租用小型游艇,各租一次.设甲、乙租用不超过两小时的概率分别为 ,
, ;租用2小时以上且不超过3小时的概率分别为
;租用2小时以上且不超过3小时的概率分别为 ,
, ,且两人租用的时间都不超过4小时.
,且两人租用的时间都不超过4小时.
(Ⅰ)求甲、乙两人所付费用相同的概率;
(Ⅱ)设甲、乙两人所付的费用之和为随机变量 ,求
,求 的分布列与数学期望.
的分布列与数学期望.
在如图所示的几何体中,四边形 是菱形,
是菱形, 是矩形,平面
是矩形,平面 ⊥平面
⊥平面 ,
, 是
是 的中点.
的中点.
(1)求证: ∥平面
∥平面 ;
;
(2)在线段 上是否存在点
上是否存在点 ,使二面角
,使二面角 的大小为
的大小为 ?若存在,求出
?若存在,求出 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.