(本小题满分10分)
设集合 ,
,
(1)求集合 ;(2)若不等式
;(2)若不等式 的解集为
的解集为 ,求
,求 的值
的值
已知向量
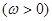 ,函数
,函数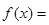
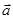 ·
·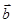 ,且最小正周期为
,且最小正周期为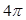 .
.
(1)求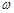 的值;
的值;
(2)设
 ,求
,求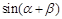 的值.
的值.
有三个新兴城镇分别位于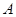 、
、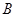 、
、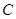 三点处,且
三点处,且 ,
,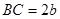 ,今计划合建一个中心医院,为同时方便三镇,准备建在
,今计划合建一个中心医院,为同时方便三镇,准备建在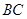 的垂直平分线上的
的垂直平分线上的 点处(建立坐标系如图).
点处(建立坐标系如图).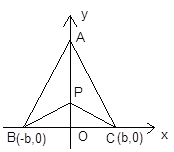
(1)若希望点 到三镇距离的平方和最小,则
到三镇距离的平方和最小,则 应位于何处?
应位于何处?
(2)若希望点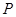 到三镇的最远距离为最小,则
到三镇的最远距离为最小,则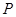 应位于何处?
应位于何处?
已知动圆过定点P(1,0),且与定直线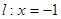 相切,点C在l上.
相切,点C在l上.
(1)求动圆圆心的轨迹M的方程;
(2)设过点P,且斜率为-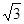 的直线与曲线M相交于A,B两点.
的直线与曲线M相交于A,B两点.
①问:△ABC能否为正三角形?若能,求点C的坐标;若不能,说明理由;
②当△ABC为钝角三角形时,求这种点C的纵坐标的取值范围.
如图,设点A和B为抛物线 上原点以外的两个动点,已知OA⊥OB,OM⊥AB求点M的轨迹方程,并说明它表示什么曲线
上原点以外的两个动点,已知OA⊥OB,OM⊥AB求点M的轨迹方程,并说明它表示什么曲线
已知椭圆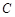 的方程为
的方程为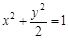 ,点
,点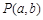 的坐标满足
的坐标满足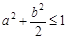 过点
过点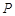 的直线
的直线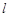 与椭圆交于
与椭圆交于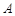 、
、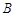 两点,点
两点,点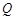 为线段
为线段 的中点,求:
的中点,求:
(1)点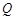 的轨迹方程;
的轨迹方程;
(2)点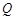 的轨迹与坐标轴的交点的个数.
的轨迹与坐标轴的交点的个数.