已知椭圆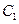 、抛物线
、抛物线 的焦点均在
的焦点均在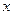 轴上,
轴上,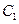 的中心和
的中心和 的顶点均为原点
的顶点均为原点 ,从每条曲线上取两个点,将其坐标记录于下表中:
,从每条曲线上取两个点,将其坐标记录于下表中:
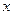 |
3 |
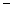 2 2 |
4 |
 |
 |
 |
0 |
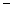 4 4 |
 |
(Ⅰ)求 的标准方程;
的标准方程;
(Ⅱ)请问是否存在直线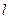 满足条件:①过
满足条件:①过 的焦点
的焦点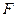 ;②与
;②与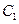 交不同两点
交不同两点 且满足
且满足 ?若存在,求出直线
?若存在,求出直线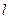 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
(本题满分14分,第1小题5分,第2小题9分)
一校办服装厂花费2万元购买某品牌运动装的生产与销售权,根据以往经验,每生产1百套这种品牌运动装的成本为1万元,每生产x(百套)的销售额R(x) (万元)满足:
(万元)满足:
(1)该服装厂生产750套此种品牌运动装可获得利润多少万元?
(2)该服装厂生产多少套此种品牌运动装利润最大?此时, 利润是多少万元?
利润是多少万元?
(本题满分14分,第1小题8分,第2小题6分)
(理)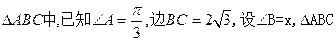 的周长为
的周长为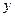 。
。
(1)求函数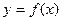 的解析式 ,并写出函数的定义域;
的解析式 ,并写出函数的定义域;
(2)求函数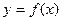 的值域。
的值域。
(文)设函数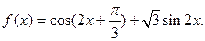
(1)求函数 的最大值和及相应的
的最大值和及相应的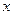 的值;
的值;
(2)设A,B,C为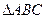 的三个内角,
的三个内角,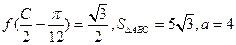 ,求角C的大小及
,求角C的大小及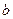 边的长。
边的长。
(本题满分12分,第1小题6分,第小题6分)
设函数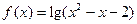 的定义域为集合A,函数
的定义域为集合A,函数 的定义域为集合B。
的定义域为集合B。
(1)求A∩B;
(2)若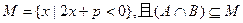 ,求实数
,求实数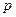 的取值范围。
的取值范围。
(本小题满分14分)已知中心在坐标原点O的椭圆C经过点A(2,3),且点F(2,0)为其右焦点。
(1)求椭圆C的方程;
(2)是否存在平行于OA的直线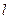 ,使得直线
,使得直线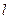 与椭圆C有公共点,且直线OA与
与椭圆C有公共点,且直线OA与 的距离等于4?若存在,求出直线
的距离等于4?若存在,求出直线 的方程;若不存在,请说明理由。
的方程;若不存在,请说明理由。
(本小题满分14分)已知 c>0, 设命题p:指数函数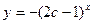 在实数集R上为增函数,命题q:不等式
在实数集R上为增函数,命题q:不等式 在R上恒成立.若命题p或q是真命题, p且q是假命题,求c的取值范围.
在R上恒成立.若命题p或q是真命题, p且q是假命题,求c的取值范围.