在课外活动时间,小王、小丽、小华做“互相踢踺子”游戏,踺子从一人传到另一人就记为踢一次.
(1)若从小丽开始,经过两次踢踺后,踺子踢到小华处的概率是多少?
(2)若从小丽开始踢,经过三次踢踺后,小丽认为踢到她的可能性最大,你同意她的观点吗?请说明理由.
四边形 的对角线交于点 ,有 , ,以 为直径的半圆过点 ,圆心为 .
(1)利用图1,求证:四边形 是菱形.
(2)如图2,若 的延长线与半圆相切于点 ,已知直径 .
①连接 ,求 的面积.
②求弧 的长.

如图,直线 与 , 轴分别交于点 , ,与反比例函数 图象交于点 , ,过点 作 轴的垂线交该反比例函数图象于点 .
(1)求点 的坐标.
(2)若 .
①求 的值.
②试判断点 与点 是否关于原点 成中心对称?并说明理由.

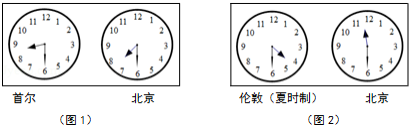
如图1表示同一时刻的韩国首尔时间和北京时间,两地时差为整数.
(1)设北京时间为 (时 ,首尔时间为 (时 ,就 ,求 关于 的函数表达式,并填写下表(同一时刻的两地时间).
|
北京时间 |
|
|
|
|
首尔时间 |
|
|
|
(2)如图2表示同一时刻的英国伦敦时间(夏时制)和北京时间,两地时差为整数.如果现在伦敦(夏时制)时间为 ,那么此时韩国首尔时间是多少?
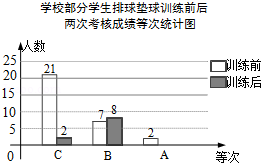
某校组织学生排球垫球训练,训练前后,对每个学生进行考核.现随机抽取部分学生,统计了训练前后两次考核成绩,并按“ , , ”三个等次绘制了如图不完整的统计图.试根据统计图信息,解答下列问题:
(1)抽取的学生中,训练后“ ”等次的人数是多少?并补全统计图.
(2)若学校有600名学生,请估计该校训练后成绩为“ ”等次的人数.
如图,在矩形 中,点 为坐标原点,点 的坐标为 ,点 、 在坐标轴上,点 在 边上,直线 ,直线 .
(1)分别求直线 与 轴,直线 与 的交点坐标;
(2)已知点 在第一象限,且是直线 上的点,若 是等腰直角三角形,求点 的坐标;
(3)我们把直线 和直线 上的点所组成的图形为图形 .已知矩形 的顶点 在图形 上, 是坐标平面内的点,且 点的横坐标为 ,请直接写出 的取值范围(不用说明理由).
