在一个不透明的盒子里装有只有颜色不同的黑、白两种球共40个,小颖做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是“摸到白球”的频率折线统计图: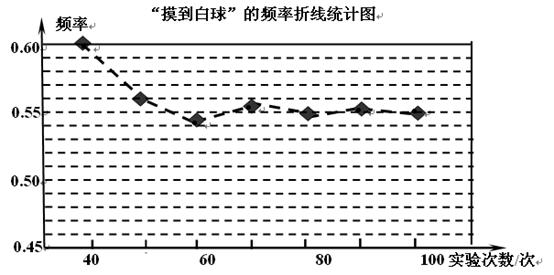
(1)请估计:当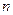 很大时,摸到白球的频率将会接近 (精确到0.01);
很大时,摸到白球的频率将会接近 (精确到0.01);
(2)假如你摸一次,你摸到黑球的概率P(黑球)= ;
(3)试估算盒子里白、黑两种颜色的球各有多 少个?
少个?
(4)在(2)条件下如果要使摸到白球的概率为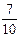 ,需要往盒子里再放入多少个白球?
,需要往盒子里再放入多少个白球?
如图,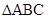 中,
中,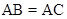 ,
,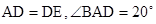 ,
,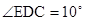 ,求
,求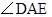 的度数?
的度数?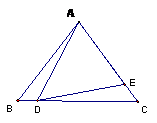
某采摘农场计划种植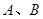 两种草莓共6亩,根据表格信息,解答下列问题:
两种草莓共6亩,根据表格信息,解答下列问题:
| 项目 品种 |
A |
B |
| 年亩产(单位:千克) |
1200 |
2000 |
| 采摘价格(单位:元/千克) |
60 |
40 |
(1)若该农场每年草莓全部被采摘的总收入为46000O元,那么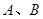 两种草莓各种多少亩?
两种草莓各种多少亩?
(2)若要求种植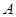 种草莓的亩数不少于种植
种草莓的亩数不少于种植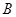 种草莓的一半,那么种植
种草莓的一半,那么种植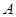 种草莓多少亩时,可使该农场每年草莓全部被采摘的总收入最多?
种草莓多少亩时,可使该农场每年草莓全部被采摘的总收入最多?
已知:如图,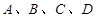 四点在同一直线上,请你从下面四项中选出三个作为条件,其余一个作为结论,构成一个真命题,并进行证明。
四点在同一直线上,请你从下面四项中选出三个作为条件,其余一个作为结论,构成一个真命题,并进行证明。
①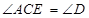 ,②
,②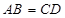 ③
③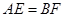 ,④
,④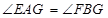
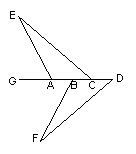
当 为何值时,方程组
为何值时,方程组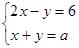 的解是正数?
的解是正数?
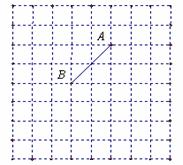
请在所给网格中按下列要求操作:
⑴ 请在网格中建立平面直角坐标系,使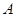 点坐标为(0,2),
点坐标为(0,2), 点坐标为(-2,0);
点坐标为(-2,0);
⑵ 在(1)的条件下,在平面坐标系中确定点C,使△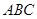 为等腰直角三角形,请画出所有符合条件的点
为等腰直角三角形,请画出所有符合条件的点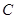 ,并直接写出相应的
,并直接写出相应的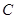 点坐标.
点坐标.