(本小题满分12分)设关于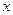 的方程
的方程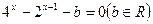
(Ⅰ)若方程有实数解,求实数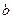 的取值范围;
的取值范围;
(Ⅱ)当方程有实数解时,讨论方程实根的个数,并求出方程的解.
(本小题满发14分)已知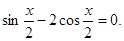
(Ⅰ)求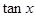 的值;
的值;
(Ⅱ)求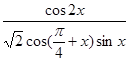 的值
的值
(本小题共13分)对于数列 ,若满足
,若满足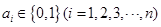 ,则称数列
,则称数列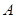 为“0-1数列”.定义变换
为“0-1数列”.定义变换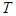 ,
,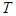 将“0-1数列”
将“0-1数列”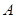 中原有的每个1都变成0,1,原有的每个0都变成1,0.例如
中原有的每个1都变成0,1,原有的每个0都变成1,0.例如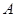 :1,0,1,则
:1,0,1,则 设
设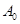 是“0-1数列”,令
是“0-1数列”,令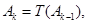
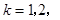 3,….
3,….
(Ⅰ) 若数列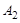 :
: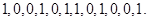 求数列
求数列 ;
;
(Ⅱ) 若数列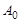 共有10项,则数列
共有10项,则数列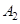 中连续两项相等的数对至少有多少对?请说明理由;
中连续两项相等的数对至少有多少对?请说明理由;
(Ⅲ)若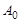 为0,1,记数列
为0,1,记数列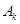 中连续两项都是0的数对个数为
中连续两项都是0的数对个数为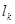 ,
,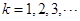 .求
.求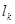 关于
关于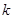 的表达式.
的表达式.
(本小题共13分)在平面直角坐标系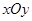 中,设点
中,设点 ,以线段
,以线段 为直径的圆经过原点
为直径的圆经过原点 .
.
(Ⅰ)求动点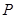 的轨迹
的轨迹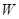 的方程;
的方程;
(Ⅱ)过点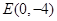 的直线
的直线 与轨迹
与轨迹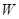 交于两点
交于两点 ,点
,点 关于
关于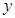 轴的对称点为
轴的对称点为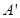 ,试判断直线
,试判断直线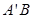 是否恒过一定点,并证明你的结论.
是否恒过一定点,并证明你的结论.
(本小题共14分)已知函数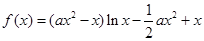 .
. .
.
(Ⅰ)当 时,求曲线
时,求曲线 在
在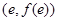 处的切线方程(
处的切线方程(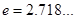 );
);
(Ⅱ)求函数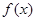 的单调区间.
的单调区间.
(本小题共14分)如图,四棱锥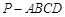 的底面是直角梯形,
的底面是直角梯形,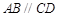 ,
,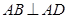 ,
,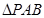 和
和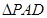 是两个边长为
是两个边长为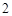 的正三角形,
的正三角形,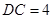 ,
,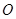 为
为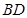 的中点,
的中点,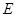 为
为 的中点.
的中点.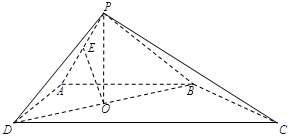
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求证: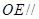 平面
平面 ;
;
(Ⅲ)求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.