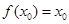平面EFGH分别平行空间四边形ABCD中的CD与AB且交BD、AD、
AC、BC于E、F、G、H.CD=a,AB=b,CD⊥AB.
(1)求证EFGH为矩形;
(2)点E在什么位置,SEFGH最大?
已知复数 ,
,
(1)当 时,求
时,求 ;
;
(2)当 为何值时,
为何值时, 为纯虚数;
为纯虚数;
(3)若复数 在复平面上所对应的点在第四象限,求实数
在复平面上所对应的点在第四象限,求实数 的取值范围。
的取值范围。
某校的研究性学习小组为了研究高中学生的身体发育状况,在该校随机抽出120名17至18周岁的男生,其中偏重的有60人,不偏重的也有60人。在偏重的60人中偏高的有40人,不偏高的有20人;在不偏重的60人中偏高和不偏高人数各占一半
(1)根据以上数据建立一个 列联表:
列联表:
| 偏重 |
不偏重 |
合计 |
|
| 偏高 |
|||
| 不偏高 |
|||
| 合计 |
(2)请问该校17至18周岁的男生身高与体重是否有关?
已知数列 的前
的前 项和为
项和为 .
.
(Ⅰ)计算 ;
;
(Ⅱ)根据(Ⅰ)所得到的计算结果,猜想 的表达式,不必证明.
的表达式,不必证明.
设函数 ,其中
,其中 .证明:当
.证明:当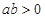 时,函数
时,函数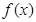 没有极值点;当
没有极值点;当 时,函数
时,函数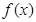 有且只有一个极值点,并求出极值.
有且只有一个极值点,并求出极值.
已知定义域为[0,1]的函数同时满足以下三个条件:①对任意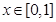 ,总有
,总有 ;②
;②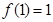 ;③若
;③若 ,则有
,则有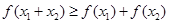 成立.
成立.
(1) 求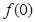 的值;(2) 函数
的值;(2) 函数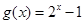 在区间[0,1]上是否同时适合①②③?并予以证明
在区间[0,1]上是否同时适合①②③?并予以证明
(3) 假定存在 ,使得
,使得 ,且
,且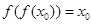 ,求证:
,求证: