某校的研究性学习小组为了研究高中学生的身体发育状况，在该校随机抽出120名17至18周岁的男生，其中偏重的有60人，不偏重的也有60人。在偏重的60人中偏高的有40人，不偏高的有20人；在不偏重的60人中偏高和不偏高人数各占一半
（1）根据以上数据建立一个
列联表：
| |
偏重 |
不偏重 |
合计 |
| 偏高 |
|
|
|
| 不偏高 |
|
|
|
| 合计 |
|
|
|
（2）请问该校17至18周岁的男生身高与体重是否有关？
已知函数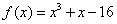
．
(Ⅰ)求曲线
在点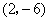
处的切线方程；
(Ⅱ)直线
为曲线的切线，且经过原点，求直线的方程及切点坐标．
已知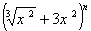
展开式各项系数的和比它的二项式系数的和大992.
（Ⅰ）求n；
（Ⅱ）求展开式中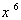
的项；
（Ⅲ）求展开式系数最大项.
观察（1）
;
（2）
;
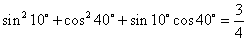（3）
.
请你根据上述规律，提出一个猜想，并证明.
有4名男生、5名女生，全体排成一行，问下列情形各有多少种不同的排法？
（Ⅰ）甲不在中间也不在两端；
（Ⅱ）甲、乙两人必须排在两端；
（Ⅲ）男、女生分别排在一起；
（Ⅳ）男女相间；
（Ⅴ）甲、乙、丙三人从左到右顺序保持一定．
（I）求函数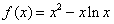
图象上的点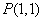
处的切线方程；
（Ⅱ）已知函数
，其中
是自然对数的底数，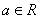
对于任意的
，
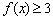恒成立，求实数
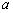的取值范围。