(眉山)(本小题满分9分)某厂为了丰富大家的业余生活,组织了一次工会活动,准备一次性购买若干钢笔和笔记本(每支钢笔的价格相同,每本笔记本的价格相同)作为奖品.若购买2支钢笔和3本笔记本共需62元,购买5支钢笔和1本笔记本共需90元.
(1)购买一支钢笔和一本笔记本各需多少元?
(2)工会准备购买钢笔和笔记本共80件作奖品,根据规定购买的总费用不超过1100元,则工会最多可以购买多少支钢笔?
(泸州)某小区为了绿化环境,计划分两次购进A、B两种花草,第一次分别购进A、B两种花草30棵和15棵,共花费675元;第二次分别购进A、B两种花草12棵和5棵.两次共花费940元(两次购进的A、B两种花草价格均分别相同).
(1)A、B两种花草每棵的价格分别是多少元?
(2)若购买A、B两种花草共31棵,且B种花草的数量少于A种花草的数量的2倍,请你给出一种费用最省的方案,并求出该方案所需费用.
(凉山州)2015年5月6日,凉山州政府在邛海“空列”项目考察座谈会上与多方达成初步合作意向,决定共同出资60.8亿元,建设40千米的邛海空中列车.据测算,将有24千米的“空列”轨道架设在水上,其余架设在陆地上,并且每千米水上建设费用比陆地建设费用多0.2亿元.
(1)求每千米“空列”轨道的水上建设费用和陆地建设费用各需多少亿元?
(2)预计在某段“空列”轨道的建设中,每天至少需要运送沙石1600m3,施工方准备租用大、小两种运输车共10辆,已知每辆大车每天运送沙石200m3,每辆小车每天运送沙石120m3,大、小车每天每辆租车费用分别为1000元、700元,且要求每天租车的总费用不超过9300元,问施工方有几种租车方案?哪种租车方案费用最低,最低费用是多少?
(资阳)学校需要购买一批篮球和足球,已知一个篮球比一个足球的进价高30元,买两个篮球和三个足球一共需要510元.
(1)求篮球和足球的单价;
(2)根据实际需要,学校决定购买篮球和足球共100个,其中篮球购买的数量不少于足球数量的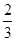 ,学校可用于购买这批篮球和足球的资金最多为10500元.请问有几种购买方案?
,学校可用于购买这批篮球和足球的资金最多为10500元.请问有几种购买方案?
(3)若购买篮球x个,学校购买这批篮球和足球的总费用为y(元),在(2)的条件下,求哪种方案能使y最小,并求出y的最小值.
(遂宁)解不等式组 ,并将解集在数轴上表示出来.
,并将解集在数轴上表示出来.