(本小题满分12分)在平面直角坐标系xOy中,有一个以为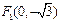 和
和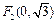 焦点、离心率为
焦点、离心率为 的椭圆.设椭圆在第一象限的部分为曲线C, 动点P在C上, C在点P处
的椭圆.设椭圆在第一象限的部分为曲线C, 动点P在C上, C在点P处
的切线与x , y轴的交点分别为A、B,且向量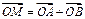 .求:
.求:
(1)点M的轨迹方程;
(2)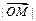 的最小值.
的最小值.
(本小题满分12分)学习小组有6个同学,其中4个同学从来没有参加过数学研究性学习活动,2个同学曾经参加过数学研究性学习活动.
(1)现从该小组中任选2个同学参加数学研究性学习活动,求恰好选到1个曾经参加过数学研究性学习活动的同学的概率;
(2)若从该小组中任选2个同学参加数学研究性学习活动,活动结束后,求该小组没有参加过数学研究性学习活动的同学个数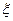 取2,3,4时的概率
取2,3,4时的概率
(本小题满分12分)如图,在棱长为2的正方体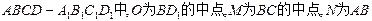 的中点,P为BB1的中点.
的中点,P为BB1的中点.
(I)求证 ;
;
(II)求异面直线 所成角的大小;
所成角的大小;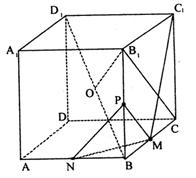
(本小题满分10分)某种有奖销售的饮料,瓶盖内印有“奖励一瓶”或“谢谢购买”字样,购买一瓶若其瓶盖内印有“奖励一瓶”字样即为中奖,中奖概率为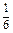 .甲、乙、丙三位同学每人购买了一瓶该饮料。
.甲、乙、丙三位同学每人购买了一瓶该饮料。
(Ⅰ)求三位同学都没有中奖的概率;
(Ⅱ)求三位同学中至少有两位没有中奖的概率.
某厂根据市场需求开发折叠式小凳(如图所示). 凳面为三角形的尼龙布,凳脚为三根细钢管. 考虑到钢管的受力和人的舒适度等因素,设计小凳应满足:① 凳子高度为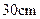 ,② 三根细钢管相交处的节点
,② 三根细钢管相交处的节点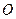 与凳面三角形
与凳面三角形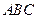 重心的连线垂直于凳面和地面. (1)若凳面是边长为
重心的连线垂直于凳面和地面. (1)若凳面是边长为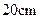 的正三角形,三只凳脚与地面所成的角均为
的正三角形,三只凳脚与地面所成的角均为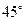 ,确定节点
,确定节点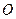 分细钢管上下两段的比值;
分细钢管上下两段的比值;
(2)若凳面是顶角为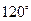 的等腰三角形,腰长为
的等腰三角形,腰长为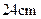 ,节点
,节点 分细钢管上下两段之比为
分细钢管上下两段之比为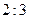 . 确定三根细钢管的长度.
. 确定三根细钢管的长度.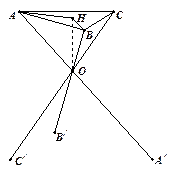
(本小题满分12分) 甲、乙两人在一场五局三胜制的象棋比赛中,规定甲或乙无论谁先赢满三局就获胜,并且比赛就此结束.现已知甲、乙两人每比赛一局甲取胜的概率是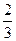 ,乙取胜的概率为
,乙取胜的概率为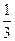 ,且每局比赛的胜负是独立的,试求下列问题:
,且每局比赛的胜负是独立的,试求下列问题:
(Ⅰ)比赛以甲3胜1而结束的概率;
(Ⅱ)比赛以乙3胜2而结束的概率;
(Ⅲ)设甲获胜的概率为a,乙获胜的概率为b,求a:b的值.