(本小题满分12分)如图,在多面体ABCDE中,AE⊥面ABC,DB//AE,且AC=AB=BC=AE=1,BD=2,F为CD中点。
(1)求证:EF⊥平面BCD;
(2)求多面体ABCDE的体积;
(3)求平面ECD和平面ACB所成的锐二面角的余弦值。
已知 是等比数列
是等比数列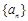 的前
的前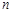 项和,
项和, ,
,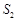 ,
, 成等差数列,且
成等差数列,且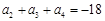 .
.
(1)求数列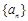 的通项公式;
的通项公式;
(2)是否存在正整数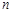 ,使得
,使得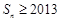 ?若存在,求出符合条件的所有
?若存在,求出符合条件的所有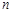 的集合;
的集合;
若不存在,说明理由.
已知 中,内角
中,内角 的对边分别为
的对边分别为 ,且
,且 ,
, .
.
(1)求 的值(2)设
的值(2)设 ,求
,求 的面积.
的面积.
以下茎叶图记录了甲、乙两组各四名同学的植树棵数。乙组记录中有一个数据模糊,无法确认,在图中经X表示。
(1)如果X=8,求乙组同学植树棵数的平均数和方差
(2)如果X=9,分别从甲、乙两组中随机选取一名同学,求这两名同学的植树总棵数为19的概率
已知函数

(1)讨论函数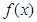 在定义域内的极值点的个数;
在定义域内的极值点的个数;
(2)若函数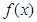 在
在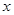 =1处取得极值,对任意的
=1处取得极值,对任意的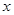 ∈(0,+∞),
∈(0,+∞),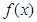 ≥
≥ 恒成立,求实数b的取值范围;
恒成立,求实数b的取值范围;
(3)当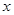 >
>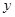 >
> 时,求证:
时,求证: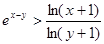
已知数列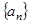 的前n项和为
的前n项和为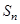 ,
,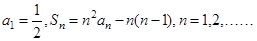
(1)证明:数列 是等差数列,并求
是等差数列,并求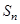 ;
;
(2)设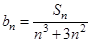 ,求证:
,求证: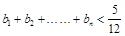 .
.