(本小题满分12分)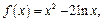
(1)求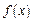 的最小值;(2)若
的最小值;(2)若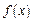 ≥
≥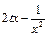 在
在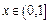 内恒成立,求
内恒成立,求 的取值范围
的取值范围
(本小题共14分)已知函数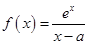 (其中常数
(其中常数 ).
).
(1)求函数 的定义域及单调区间;
的定义域及单调区间;
(2)若存在实数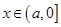 ,使得不等式
,使得不等式 成立,求
成立,求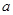 的取值范围.
的取值范围.
(本小题共13分)已知△ABC的三个内角A,B,C的对边分别为a,b,c,且△ABC的面积为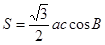 ,
,
(1)若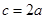 ,求角A,B,C的大小;
,求角A,B,C的大小;
(2)若a=2,且 ,求边c的取值范围.
,求边c的取值范围.
(本小题共13分)已知函数 ,
,
(1)求实数 的值;
的值;
(2)求函数 的最小正周期及单调增区间.
的最小正周期及单调增区间.
(本小题共13分)已知在等比数列 中,
中, ,且
,且 是
是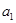 和
和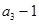 的等差中项.
的等差中项.
(1)求数列 的通项公式;
的通项公式;
(2)若数列 满足
满足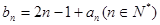 ,求
,求 的前
的前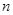 项和
项和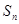 .
.
已知指数函数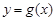 满足:
满足: ,定义域为
,定义域为 的函数
的函数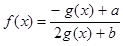 是奇函数。
是奇函数。
(1)求 ,
, 的值;
的值;
(2)判断函数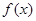 的单调性并用定义加以证明;
的单调性并用定义加以证明;
(3)若对任意的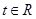 ,不等式
,不等式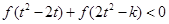 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。