(10分) 已知函数 在区间
在区间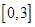 上有最小值-2,求实数a 的值
上有最小值-2,求实数a 的值
已知数列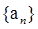 满足:
满足: ,
,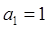 ,
, 为公差为4等差数列.数列
为公差为4等差数列.数列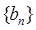 的前n项和为
的前n项和为 ,且满足
,且满足 .
.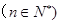
①求数列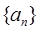 的通项公式
的通项公式 ;
;
②试确定 的值,使得数列
的值,使得数列 是等差数列;
是等差数列;
③设数列 满足:
满足:
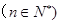 ,若在
,若在 与
与 之间插
之间插
入n个数,使得这 个数组成一个公差为
个数组成一个公差为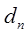 的等差数列.
的等差数列.
求证: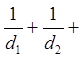 ……
…… 。
。
铁路托运行李,从甲地到乙地,规定每张火车票托运行李不超过50公斤时,每公斤0.2元,超过50公斤时,超过部分按每公斤0.3元计算,(不足1公斤时按1公斤计费),试设计一个计算某人坐火车托运行李所需费用的算法,要求画出框图,并用基本语句写出算法。
(提示: INT(x)表示取不大于x的最大整数,如INT(3.5)="3" ,INT(6)=6)
右图是计算首项为1的数列 前m项和
前m项和 的算法框图,
的算法框图,
(1)判断m的值;
(2)试写出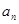 与
与 的关系式;
的关系式;
(3)根据框图分别利用For语句和Do Loop语句写出算法程序;
(4)在电脑上运行此程序,最后输出的结果是多少?
某企业的某种产品产量与单位成本统计数据如下:
| 月份 |
1 |
2 |
3 |
4 |
5 |
6 |
| 产量(千件) |
2 |
3 |
4 |
3 |
4 |
5 |
| 单位成本(元/件) |
73 |
72 |
71 |
73 |
69 |
68 |

(用最小二乘法求线性回归方程系数公式
注: ,
, )
)
(1)试确定回归方程;
(2)指出产量每增加1 件时,单位成本下降多少?
(3)假定产量为6 件时,单位成本是多少?单位成本为70元/件时,产量应为多少件?