(本小题满分12分)
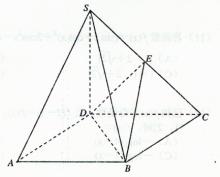
如图,在四棱锥S—ABCD中, 底面ABCD,底面ABCD是平行四边形,
底面ABCD,底面ABCD是平行四边形, ,E是SC的中点。
,E是SC的中点。
(I)求证:SA//平面BDE;
(II)求证: ;
;
(III)若SD=2,求二面角E—BD—C的余弦值。
已知等比数列{an}的所有项均为正数,首项a1=1,且a4,3a3,a5成等差数列.
(1)求数列{an}的通项公式;
(2)数列{an+1-λan}的前n项和为Sn,若Sn=2n-1(n∈N*),求实数λ的值.
设数列{an}的各项都为正数,其前n项和为Sn,已知对任意n∈N*,Sn是a和an的等差中项.
(1)证明数列{an}为等差数列,并求数列{an}的通项公式;
(2)证明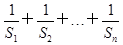 <2.
<2.
已知等差数列{an}的公差d=1,前n项和为Sn.
(1)若1,a1,a3成等比数列,求a1;
(2)若S5>a1a9,求a1的取值范围.
已知数列{an}中,a1=1,an+1=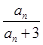 (n∈N*).
(n∈N*).
(1)求数列{an}的通项an;
(2)若数列{bn}满足bn=(3n-1) an,数列{bn}的前n项和为Tn,若不等式(-1)nλ<Tn对一切n∈N*恒成立,求λ的取值范围.
an,数列{bn}的前n项和为Tn,若不等式(-1)nλ<Tn对一切n∈N*恒成立,求λ的取值范围.
已知正项数列{an},其前n项和Sn满足6Sn= +3an+2,且a1,a2,a6是等比数列{bn}的前三项.
+3an+2,且a1,a2,a6是等比数列{bn}的前三项.
(1)求数列{an}与{bn}的通项公式;
(2)记Tn=a1bn+a2bn-1+…+anb1,n∈N*,证明:3Tn+1=2bn+1-an+1(n∈N*).