已知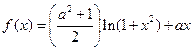

 .
.
(1)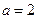 时,求
时,求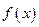 的极值
的极值
(2)当 时,讨论
时,讨论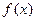 的单调性。
的单调性。
(3)证明: (
(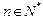 ,
,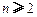 ,其中无理数
,其中无理数 )
)
已知椭圆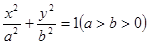 的右焦点为
的右焦点为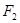 (3,0),离心率为
(3,0),离心率为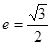 。
。
(1)求椭圆的方程。
(2)设直线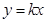 与椭圆相交于A,B两点,M,N分别为线段
与椭圆相交于A,B两点,M,N分别为线段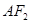 ,
,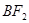 的中点,若坐标原点O在以MN为直径的圆上,求
的中点,若坐标原点O在以MN为直径的圆上,求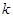 的值。
的值。
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,AP=AB,BP=BC=2,E,F分别是PB,PC的中点。
(1)证明:EF∥平面PAD;
(2)求三棱锥E-ABC的体积V。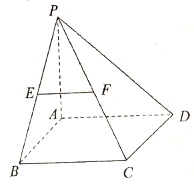
已知Rt△ABC的顶点坐标A(-3,0),直角顶点B(-1,-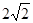 ),顶点C在
),顶点C在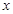 轴上。
轴上。
(1)求BC边所在直线的方程;
(2)圆M为Rt△ABC外接圆,其中M为圆心,求圆M的方程;
(3)直线 与Rt△ABC外接圆相切于第一象限,求切线与两坐标轴所围成的三角形面积最小时的切线方程。
与Rt△ABC外接圆相切于第一象限,求切线与两坐标轴所围成的三角形面积最小时的切线方程。
已知O为坐标原点,△AOB中,边OA所在的直线方程是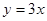 ,边AB所在的直线方程是
,边AB所在的直线方程是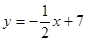 ,且顶点B的横坐标为6。
,且顶点B的横坐标为6。
(1)求△AOB中,与边AB平行的中位线所在直线的方程;
(2)求△AOB的面积;
(3)已知OB上有点D,满足△AOD与△ABD的面积比为2,求AD所在的直线方程。
定义:如果数列 的任意连续三项均能构成一个三角形的三边长,则称
的任意连续三项均能构成一个三角形的三边长,则称 为“三角形”数列.对于“三角形”数
为“三角形”数列.对于“三角形”数 列
列 ,如果函数
,如果函数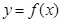 使得
使得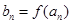 仍为一个“三角形”数列,则称
仍为一个“三角形”数列,则称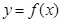 是数列
是数列 的“保三角形函数”,
的“保三角形函数”,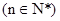 .
.
(Ⅰ)已知 是首项为2,公差为1的等差数列,若
是首项为2,公差为1的等差数列,若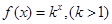 是数列
是数列 的“保三角形函数”,求k的取值范围;
的“保三角形函数”,求k的取值范围;
(Ⅱ)已知数列 的首项为2010,
的首项为2010,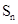 是数列
是数列 的前n项和,且满足
的前n项和,且满足 ,证明
,证明 是“三角形”数列;
是“三角形”数列;
(Ⅲ)根据“保三角形函数”的定义,对函数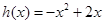 ,
, ,和数列1,
,和数列1,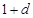 ,
,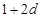 ,(
,( )提出一个正确的命题,并说明理由.
)提出一个正确的命题,并说明理由.